Параллельность прямой и плоскости

Плоскость и прямая, не лежащая в этой плоскости, называются параллельными, если они не пересекаются, сколько бы их не продолжали.

Параллельность прямой и плоскости может быть установлена одним из следующих двух способов:

1. Через данную прямую надо провести произвольную плоскость (проще одну из проецирующих) и построить линию ее пересечения с заданной плоскостью. Если полученная линия пересечения плоскостей окажется параллельной данной прямой можно утверждать, что прямая параллельна данной плоскости;

2. Через произвольную точку, принадлежащую этой плоскости, надо провести прямую, параллельную данной прямой. Если окажется, что прове­денная прямая будет принадлежать данной плоскости, следует заключить, что прямая параллельна данной плоскости.

Задача 1. Через данную точку А провести прямую m, параллельную плоскости a.

Для того, чтобы прямая была параллельна плоскости, она должна быть параллельна какой-нибудь прямой, принадлежащей этой плоскости, а потому, взяв в плоскости a
(рис. 5.3) произвольную прямую n, проведем через точку А прямую m, ей параллельную.

Рис. 5.3	Рис. 5.4

Задача 2. Через данную прямую а провести плоскость a, параллельную данной прямой m (рис. 5.4).

Через точку К, взятую на прямой а, проведем прямую b, параллельную данной прямой m. Плоскость, образованная пересекающимися прямыми а и b, будет искомой.

Перпендикулярность прямой и плоскости

На рис. 5.5 изображена плоскость a и перпендикулярная к ней прямая n.

Рис. 5.5	Рис. 5.6

Прямая n перпендикулярнак любой прямой плоскости a, т. е. n ^ a,
n ^ b, n ^ h, n ^ f. Каждый такой прямой угол проецируется на плоскость проекций в виде некоторого угла, но угол между прямой n и горизонталью плоскости h проецируется на горизонтальную плоскость проекций прямым углом, так как его сторона h ||p_1. Угол между прямой n и фронталью f плоскости проецируется на фронтальную плоскость проекций прямым углом (его сторона f ||p₂).

В том случае, когда плоскость задана следами (рис. 5.6), проекции перпендикуляра располагаются перпендикулярно, к одноименным следам плоскости: n ′^ h ′_0α, n "^ f ′ _0α. Если прямая перпендикулярна к плоскости, то ее проекции перпендикулярны к одноименным проекциям одноименных линий уровня, а также одноименным следам этой плоскости. Справедливо и обратное положение: если плоскость перпендикулярна прямой, то ее следы, а также проекции линий уровня перпендикулярны одноименным проекциям прямой.

На рис. 5.7 через точку N проведена прямая n, перпендикулярная к плоскости a. Для этого в плоскости a(а ∩ b) определены горизонталь h и фронталь ¦ и горизонтальная проекция перпендикуляра проведена перпен­дикулярно к горизонтальной проекции горизонтали, а фронтальная проекция – перпендикулярно к фронтальной проекциям фронтали: n ¢^ h ¢, n ¢¢^¦¢¢.

Плоскость, перпендикулярную к данной прямой, определяют с помощью пересекающихся линий уровня. На рис. 5.8 через точку B проведена плоскость a, перпендикулярная к заданной прямой n. Горизонталь h плоскости a проходит через точку B (h É B, h ¢ ^ n ¢). Фронталь этой плоскости также проходит через точку В (¦ 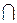h = B, ¦ ²^ n ²).

На рис. 5.9 показана прямая, перпендикулярная к горизонтально проецирующей плоскости. Эта линия является горизонталью.

На рис. 5.10 изображена прямая, перпендикулярная к фронтально проецирующей плоскости. Она является фронталью.

На рис. 5.11 изображена прямая n (MN), перпендикулярная к профильно проецирующей плоскости g. Проведя проекции n ¢¢^ f ¢¢ и n ¢^ h ¢, мы еще не определим искомого перпендикуляра, так как перпендикулярность прямой и плоскости обеспечивается перпендикулярностью этой прямой к двум пересекающимся прямым плоскости. Для решения этой задачи нужно построить профильную прямую плоскости и провести n ¢¢¢^ p ¢¢¢ или найти профильный след, тогда n ¢¢¢^ g¢¢¢.

Рис. 5.7	Рис. 5.8
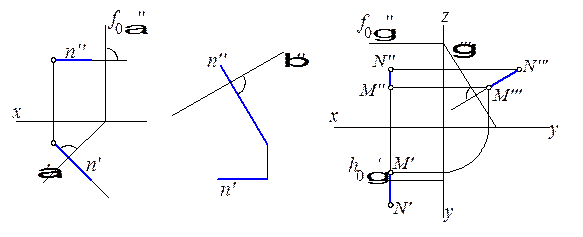
Рис. 5.9	Рис. 5.10	Рис. 5.11

Дата добавления: 2014-01-14