
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема (формула Бернулли)
|
|
|
|
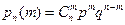 ,
,
где 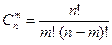 - число сочетаний из
- число сочетаний из  по
по  ,
, 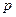 - вероятность события
- вероятность события 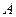 ,
, 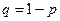 - вероятность события
- вероятность события  (т.е. вероятность не наступления события
(т.е. вероятность не наступления события 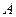 ).
).
Доказательство. Начнём с малого. Пусть  обозначает исходное событие, т.е. появление ровно
обозначает исходное событие, т.е. появление ровно  раз события
раз события 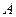 в
в  независимых испытаниях (вероятность появления
независимых испытаниях (вероятность появления 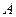 в одном испытании, напомню, равняется
в одном испытании, напомню, равняется 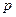 ).
).
Событие 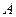 может, например, появиться (событие
может, например, появиться (событие  ) следующим образом: вначале испытаний событие
) следующим образом: вначале испытаний событие 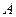 наступает ровно
наступает ровно  раз, а затем оно
раз, а затем оно  раз не наступает (значит, наступит противоположное событие
раз не наступает (значит, наступит противоположное событие  ):
):
 .
.
Найдём вероятность этого события. Поскольку все события независимы («вероятность произведения равна произведению вероятностей»), то:
 .
.
А вероятность  найдём исхитрившись. События
найдём исхитрившись. События 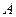 и
и  образуют полную группу, т.е.
образуют полную группу, т.е.
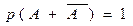 .
.
Кроме того, они несовместны (т.к. вместе произойти не могут). Поэтому («вероятность суммы равна сумме вероятностей»):
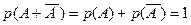 ,
,
Откуда:
 .
.
Поэтому
 .
.
Но событие 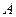 может появиться и другим образом. Например,
может появиться и другим образом. Например,
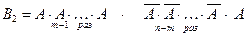 .
.
Нетрудно убедиться в том, что вероятность  по-прежнему равна:
по-прежнему равна:
 .
.
Но как пересчитать все эти возможности (ясно, что они все являются несовместными, а поэтому 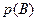 будет равно числу (сумме) всех этих возможностей умноженной на
будет равно числу (сумме) всех этих возможностей умноженной на  )? Число всех возможных таких вариантов событий
)? Число всех возможных таких вариантов событий  равно
равно 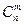 , числу способов, которыми можно расположить
, числу способов, которыми можно расположить  чисел по
чисел по  местам (при этом порядок, занимаемый числами, не имеет значение):
местам (при этом порядок, занимаемый числами, не имеет значение):
числа  располагаются по
располагаются по  местам (событие
местам (событие 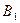 ),
),
числа  располагаются по
располагаются по  местам (событие
местам (событие 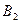 ),
),
и т.д.
Поэтому
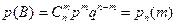 .
.
Что и требовалось доказать.
_______________
Пример. Для нормальной работы автобазы на линии должно быть не менее восьми автомашин, на автобазе всего десять машин. Вероятность невыхода каждой автомашины на линию равна  . Найти вероятность нормальной работы автобазы.
. Найти вероятность нормальной работы автобазы.
Решение. Прежде всего поймём, что значит вероятность нормальной работы автобазы:
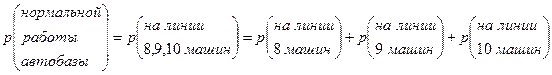 .
.
Причём последнее равенство справедливо, т.к. несовместными являются события «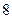 машин на линии», «
машин на линии», «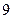 машин на линии» и «
машин на линии» и « машин на линии».
машин на линии».
Вероятность того, что 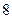 автомашин на линии, равна «вероятности того, что в
автомашин на линии, равна «вероятности того, что в  независимых испытаниях событие
независимых испытаниях событие 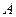 (выход одной машины на линию) наступит ровно
(выход одной машины на линию) наступит ровно 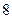 раз»
раз»
 ,
,
где 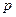 - вероятность выхода одной машины на линию, а
- вероятность выхода одной машины на линию, а  - вероятность невыхода одной машины на линию. Поскольку по условию задачи
- вероятность невыхода одной машины на линию. Поскольку по условию задачи  , постольку
, постольку  . Окончательно,
. Окончательно,
 .
.
Аналогично:
 и
и  .
.
Поэтому:
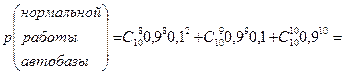
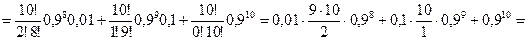
 .
.
Сделаем вывод. Поскольку в статистике считается, что событие, вероятность которого «больше 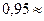 достоверное событие», постольку базу, иногда, будет «лихорадить». Полностью нормальной её работу считать нельзя! А для исправления ситуации следует прикупить автомашины или поработать над уменьшением вероятности «невыхода каждой автомашины на линию».
достоверное событие», постольку базу, иногда, будет «лихорадить». Полностью нормальной её работу считать нельзя! А для исправления ситуации следует прикупить автомашины или поработать над уменьшением вероятности «невыхода каждой автомашины на линию».
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 1252; Нарушение авторских прав?; Мы поможем в написании вашей работы!