Суть графического метода

По направлению (против направления) С в области допустимых решений производится поиск оптимальной точки: Х*(х1*,х2*). Оптимальной мы будем считать точки, через которые проходит линия уровня L max(L min) и соответствующая наибольшим(наименьшим) значениям функции L(х). Оптимальное решение всегда находится на границе ОДР. (Как правило, это одна из вершин многоугольника ОДР, через которую будет проходить целевая функция, или же вся его сторона.)

L(x) = L2 Линии уровня

(1) Ах1Х1 + Ах2Х2 ≥ Вк

(2)

1 – L = l1x1 + l2x2 в 3 вершинах

(1)

L(x) = L3

L(x) = L1

При поиске оптимального решения возможна следующая ситуация:

1. Существует единственное решение

2. Не существует, задача не имеет решение

3. Бесконечное множество решений – альтернативный оптимум – оптимальная прямая совпадает с 1 из сторон многоугольника.

4. Целевая функция неограниченна.

5. ОДР – 1 точка.

Методика решения задач линейного программирования графическим методом. Алгоритм.

1. В ограничениях поставленной задачи заменяются знаки неравенств на знаки точных равенств, и рисуем полученные прямые.
2. Находим и заштриховываем полуплоскости, разрешенным каждым из ограничений неравенств задачи, для чего мы подставляем в конкретные неравенства координаты какой либо точки и проверяем истинность полученного неравенства. Если неравенство неистинное, то мы заштриховываем полуплоскость, содержащую данную точку. Х1, Х2 всегда больше 0 – по условию накладываем ограничения.
3. Определяем область ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям и выделяем ее.
4. Если ОДР непустое множество, то строится целевая прямая (знание функции).
5. Строится вектор С, начало которого в координатах (0.0) и конец в (С1,С2). (должен быть перпендикулярен прямой целевой функции)
6. При поиске максимальной целевой функции мы передвигаемся в направлении С, если минимум – то в п/п направлении. Полученная по координатам движения вершина ОДР будет точкой мах или min, если такой вершины точки не будет, то целевая функция не ограничена на множестве сверху(д/мах) и снизу (д/min).
7. Определяются координаты точки мах или min (Х*) и вычисляется значение целевой функции в данной точке и (Х*). Для вычисления координат оптимальной точки Х* решается система уравнений прямых, по которой находится Х*.

L(x) = 3x1+2x2 следовательно мах

Х1+Х2≤6 Х1+2Х2=6 (1)

2Х1+Х2≤8 2Х1+Х2=8 (2)

-Х1+Х2≤1 -Х1+Х2=1 (3)

Х1,Х2≥0 Х2=2 (4)

(1) Х1=0 Х1=6

Х2=3 Х2=0

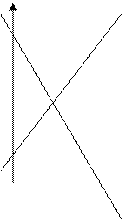8 (3)

6 С (3,2)

3 Д (4)

2 С

1 В Е

А 1 2 3 F 4 5 6 7 8

(1)

(2)

Точка Е – последняя вершина многоугольника допустимых решений, через которую проходит целевая прямая, двигаясь по направлению движения вектора С.

Точка Е (3 1/3, 1 1/3) Х1+Х2 = 6 Х1=3 1/3 = 10/3

2Х1+Х2=8 Х2=1 1/3 = 4/3

L = 3-Х1+2Х2 = 12 2/3

Дата добавления: 2014-01-14