Методика графического анализа чувствительности оптимальных решений

Для решения задачи анализа чувствительности, ограничения линейной модели классифицируются следующим образом: выделяются связывающие ограничения, проходящие через оптимальную точку, и не связывающие ограничения, не проходящие через оптимальную точку.

Дефицитный ресурс – ресурс, представленный связывающими ограничениями.

Избыточное ограничение – то ограничение, исключение которого не влияет на область ОДР и, следовательно, на оптимальное решение.

Выделяют 3 задачи анализа на чувствительность:

1-ая Задача.

Заключается в анализе сокращения или увеличения ресурсов – 2 подзадачи:

1)Насколько можно увеличить запас дефицитного ресурса для улучшения оптимального значения целевой функции

2) Насколько можно уменьшить запас недефицитного ресурса при сохранении оптимального значения целевой функции.

2-ая Задача.

Увеличение запаса какого из ресурсов наиболее выгодно.

3-ая Задача.

Анализ изменения коэффициентов целевой функции, т.е. каков диапазон изменения коэффициентов целевой функции, при которой не меняется оптимальное решение.

1. Анализ на чувствительность правой части ограничения. Ограничения 1 и 2 являются связывающими, а соответственно ресурсы - дефицитными. Это означает, что при производстве красок запасы ингредиентов А и В расходуются полностью и поэтому невозможно дальнейшее наращивание производства. В этом заключается экономический смысл понятия дефицитности ресурсов. Т.е. если фирма может увеличить суточный запас ингредиентов, то это позволит увеличить выпуск красок. Перед нами встает вопрос: до какого уровня целесообразно увеличивать запасы ингредиентов и насколько при этом увеличится оптимальное производство красок.

Правила:

1)Чтобы графически определить, как увеличить запас дефицитного ресурса, вызывающего улучшение оптимального решения, необходимо передвигать соответствующую прямую в направлении улучшения целевой функции до тех пор, пока ограничение не станет избыточным.

2)Чтобы определить максимальное уменьшение запаса недефицитного ресурса, не меняющее оптимальное решение, необходимо передвигать соответствующую прямую до пересечения с оптимальной.

3)Чтобы численно определить минимум величины запаса недефицитного ресурса, не меняющего оптимальное решение необходимо подставить координаты оптимальной точки в левую часть соответствующего ограничения.

К улучшению оптимального решения, то есть к увеличению суточного дохода приводит увеличение дефицитных ресурсов. Для определения выгодности увеличения этих ресурсов используют понятие ценности дополнительной единицы i-ого ресурса у_i

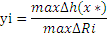
где ∆h(x*) –максимальное приращение оптимального значения целевой функции.

max∆R_i – максимально допустимый прирост объема i-ого ресурса.

Из правила следует: увеличение не суточного запаса ингредиента А на 1т. Позволяет получить доход = 3⅓ тыс.руб.,а ресрса В - 1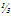тыс.руб..

Недефицитные ресурсы не имеют ценности, их изменение не приводит к увеличению дохода.

Изменение цен на продукцию, т.е. изменению коэффициентов целевой функции представляется на графике вращением прямой целевой функции вокруг оптимальной точки. При увеличении коэффициента С₁ и уменьшении коэффициента С₂ целевая прямая вращается по часовой стрелке. При таких поворотах вокруг точки она будет оставаться оптимальной до тех пор, пока наклон целевой функции прямой не выйдет за пределы, определяемые наклонами прямых ограничений (1) и (2).

4.7. Транспортная задача

Транспортные задачи описывают перемещения какого либо товара из пункта отправления (предложение) в пункт назначения (спрос).

Назначение: определение объемов перевозок с определением Min å стоимости перевозок. При этом учитывается ограничение, которое накладывается на объемы грузов в пунктах отправления и ограничения на потребность грузов в пунктах назначения.

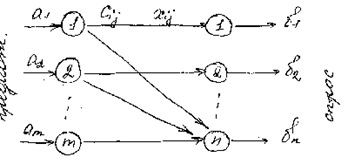
C_ij – стоимость перевозок

X_ij – кол-во перевоз.

i – обьем в пункте отправления

j – объем в пункте назначения

Общая задача – определить неизвестные величины X_ij, которые min å транспортные расходы и удовлетворяют ограничениям накладываемым на объемы грузов в пунктах отправления и пунктах назначения.

Когда å объем предложений не равен общему объему спроса, транспортная модель является несбалансированной. Для сбалансированной ввод фиктивные пункты назначения или отправления

Задача.

Т - пункт отправления. (А₁…А_т)

а₁…а_т - количество груза в каждом пункте отправление

П - пункт назначения. (В₁…В_п)

в₁…в_п – количество единичного груза, на которые подали заявки пункты назначения

(*)

c_ij – стоимость перевозки груза из Ai в Вj

(1)

Надо составить план, в соответствии, с которыми перевозки будут осуществлены за min цену.

х_ij – количество единиц груза перезенных из Аi в Вj.

(2)

совокупность чисел матрицы (2) – план перевозки

Условия:

1) Суммарное количество грузов из пункта отправления в пункт назначения равно количеству запросов в пункт отправления

(3)

2) Суммарное количество грузов, которое может вести в пункт назначения равно количеству заявок

(4)

3) Суммарная стоимость перевозок сводится к минимуму

Уравнение (3) и (4) не являются линейно независимыми, т.к. на них наложено условие (*)

Число линейно независимых уравнений m+n-1 (число базисных переменных)

m*n- число переменных xij

mn-(m+n-1) – число свободных переменных

(m-1)(n-1)

оптимальное решение k=(m-1)(n-1)=0

план будет считаться допустимым, если удовлетворяет условиям 1 и 2.

Дата добавления: 2014-01-14