
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение максвелла в комплексной форме
|
|
|
|
1 первое уравнение Максвелла
В соответствии с представлением гармонического колебания вектор
 =
=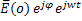 =
= ; (1.32)
; (1.32)
𝜑-начальная фаза колебаний
 - комплексная амплитуда.
- комплексная амплитуда.
Аналогично представляют другие векторы ЭМП.
1-ое уравнение Максвелла в комплексной форме имеет вид
rot
 =σ
=σ
 +jw
+jw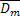
 ; (1.33)
; (1.33)
Операция дифференцирования в комплексной форме заменяется на jw/
1-ое уравнение Максвелла относительно комплексных амплитуд может быть записано так:
rot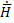 = σ
= σ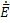 +jw
+jw ; (1.34)
; (1.34)
В полном виде оно записывается
rot =σ+jw
=σ+jw ; (1.35)
; (1.35)
1.34, 1.35-1-ое уравнение Максвелла в комплексной форме.
Преобразуем уравнение 1.35 чтобы правая часть одночленной:
rot =(σ+jw
=(σ+jw )
)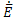 =jw
=jw (1.35a)
(1.35a)
где:
 ; (1.36)
; (1.36)
 –коплексная диэлектрическая проницаемость среды, в которой распространяется ЭМП.
–коплексная диэлектрическая проницаемость среды, в которой распространяется ЭМП.
Преобразуем уравнение 1.36, введя обозначения.
tgδ=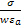 ; (1.37)
; (1.37)
– тангенс угла диэлектрических полей.
Физически он означает соотношение между амплитудами токов производимости и тока смещения.
Тогда 1.36 с учетом 1.37 Записывается
 ; (1.38)
; (1.38)
Если tgδ=0, то 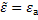 - действительная величина в этом случае потерь распространении нет.
- действительная величина в этом случае потерь распространении нет.
Уравнение 1.36 и 1.38 записываются еще в другой форме
Формула (1.39)
Tgδ= (1.40)
(1.40)

-абсолютная диэлектрическая проницаемость вакуума.
В 1961 г. Принята международная практическая система единиц СИ.
2 Второе уравнение Максвелла
Записывается в виде
rot (1.41)
(1.41)
В общем случае магнитные материалы обладают потерями. В этом случае
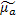 =
= -j
-j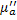
 характеризует потери в магнитных средах.
характеризует потери в магнитных средах.
где  =4π*
=4π*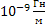 - абсолютная магнитная проницаемость не магнитных материалов и сред.
- абсолютная магнитная проницаемость не магнитных материалов и сред.
3 Полная система уравнений Максвелла в комплексной форме имеет вид:
rot = jw
= jw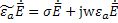 ; (1.42а)
; (1.42а)
div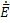 =-jw
=-jw ; (1.42б)
; (1.42б)
div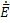 =
=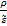 ; (1.42в)
; (1.42в)
div =0; (1.42г)
=0; (1.42г)
Если пространство имеет первичные источники- сторонние источники, то в первое уравнение Максвелла 1.42а добавляется член, характеризующий эти источники и уравнение принимает вид:
rot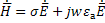 +
+ (1.43), при этом
(1.43), при этом  .
.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 532; Нарушение авторских прав?; Мы поможем в написании вашей работы!