
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Представление о случайных процессах
|
|
|
|
Тема 4. ЭЛЕМЕНТЫ ТЕОРИИ МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Рабочая тетрадь
Тема 5
Тема 4
ЭЛЕМЕНТЫ ТЕОРИИ МАРКОВСКИХ
СЛУЧАЙНЫХ ПРОЦЕССОВ
ЭЛЕМЕНТЫ ТЕОРИИ СИСТЕМ
МАССОВОГО ОБСЛУЖИВАНИЯ
студента_______________________________________________
факультета___________ отделения ___________группы________
Составитель: Е.Ю. Лискина, канд. физ.-мат. наук, доцент
Рязань 2005
СОДЕРЖАНИЕ
Тема 4. ЭЛЕМЕНТЫ ТЕОРИИ МАРКОВСКИХ
СЛУЧАЙНЫХ ПРОЦЕССОВ.......................................................................... 3
§ 1. ПРЕДСТАВЛЕНИЕ О СЛУЧАЙНЫХ ПРОЦЕССАХ................................... 3
§ 2. ОСНОВНЫЕ ПОНЯТИЯ МАРКОВСКИХ
СЛУЧАЙНЫХ ПРОЦЕССОВ............................................................................. 4
§ 3. ЦЕПИ МАРКОВА................................................................................................ 5
§ 4. НЕПРЕРЫВНЫЕ ЦЕПИ МАРКОВА................................................................ 8
4.1 Основные определения...................................................................................... 8
4.2. Финальные вероятности состояний............................................................. 10
4.3. Необходимые и достаточные условия
существования финальных вероятностей................................................... 13
4.4. Потоки событий............................................................................................... 14
Практическое занятие. Марковские процессы................................................... 16
Тема 5. ЭЛЕМЕНТЫ ТЕОРИИ СИСТЕМ
МАССОВОГО ОБСЛУЖИВАНИЯ.............................................................. 19
§ 1. КОМПОНЕНТЫ И КЛАССИФИКАЦИЯ
СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ............................................... 19
1.1. Компоненты системы массового обслуживания....................................... 19
1.2. Классификация систем массового обслуживания..................................... 22
§ 2. ОДНОКАНАЛЬНЫЕ СИСТЕМЫ
МАССОВОГО ОБСЛУЖИВАНИЯ................................................................. 23
2.1. Одноканальная СМО с отказами.................................................................. 24
2.2. Одноканальная СМО с ожиданием
и ограниченной длиной очереди.................................................................. 25
2.3. Одноканальная СМО с ожиданием
и неограниченной длиной очереди.............................................................. 29
§ 3. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ
МАССОВОГО ОБСЛУЖИВАНИЯ................................................................. 31
3.1. Многоканальная СМО с отказами................................................................ 31
3.2. Многоканальная СМО с ожиданием
и неограниченной длиной очереди............................................................. 34
Практическое занятие.
Элементы теории систем массового обслуживания........................................ 37
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.................................................... 39
Определение 1. Величина 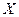 называется случайной, если она в результате опыта (реализации определённого комплекса условий) может принять тот или иное значение, причём до испытания неизвестно, какое именно.
называется случайной, если она в результате опыта (реализации определённого комплекса условий) может принять тот или иное значение, причём до испытания неизвестно, какое именно.
Определение 2. Функция  называется случайной, если её значение при любом аргументе
называется случайной, если её значение при любом аргументе 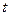 является случайной величиной.
является случайной величиной.
Определение 3. Случайная функция  , аргументом которой является время, называется случайным процессом.
, аргументом которой является время, называется случайным процессом.
Замечание. С другой стороны случайным процессом (стохастическим или вероятностным) называют процесс изменения во времени состояния какой-либо системы в соответствии с вероятностными закономерностями.
Примеры: броуновское движение частицы, турбулентные течения жидкостей и газов, распространение радиоволн в пространстве при наличии помех, движение транспортных потоков, поступление вызовов на телефонную станцию и т.д.
Теория случайных процессов – раздел теории вероятностей, изучающий зависимость случайных явлений (случайных функций) от времени и их свойства, а также разрабатывающий методы их прогнозирования и управления.
Классификация случайных процессов
| № | Признак | Класс | Случайный процесс | |
| 1. | Характер изменения аргумента 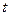
| а | дискретный | Случайные последовательности (временные ряды) |
| б | непрерывный | |||
| 2. | Характер изменения значений 
| а | дискретный | |
| б | непрерывный | |||
Характер зависимости между различными значениями  в различные моменты времени в различные моменты времени 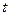
| а | В любые различные моменты времени  и и 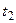 случайные величины случайные величины 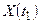 и и 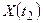 независимы. независимы.
| Случайный процесс с независимыми значениями. | |
| б | Для любых непересекающихся промежутков времени 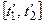 и и 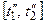 ( (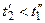 ) случайные величины ) случайные величины 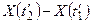 и и  независимы. независимы.
| Случайный процесс с независимыми приращениями. | ||
| в | Случайный процесс  в любой момент времени в любой момент времени 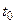 определяет распределение вероятностей, относящееся к будущему процесса. определяет распределение вероятностей, относящееся к будущему процесса.
| Марковские процессы (процессы без последействия) | ||
| г | Вероятностные характеристики случайного процесса неизменны во времени | Стационарные случайные процессы | ||
| д | Если известно процесса до момента времени 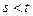 , то условное математическое ожидание процесса , то условное математическое ожидание процесса  равно равно 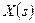 . .
| Мартингалы |
§ 2. ОСНОВНЫЕ ПОНЯТИЯ МАРКОВСКИХ
СЛУЧАЙНЫХ ПРОЦЕССОВ
Определение 1. Случайный процесс  , протекающий в какой-либо системе, называется марковским процессом или процессом без последействия, если он обладает следующим свойством: если заданы все значения
, протекающий в какой-либо системе, называется марковским процессом или процессом без последействия, если он обладает следующим свойством: если заданы все значения  при
при 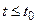 , то условное распределение
, то условное распределение 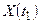 при
при 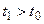 зависит только от
зависит только от 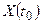 .
.
Другими словами, для любого момента времени 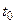 вероятность любого состояния системы в будущем (при
вероятность любого состояния системы в будущем (при 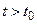 ) зависит только от её состояния в настоящем (при
) зависит только от её состояния в настоящем (при 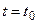 ) и не зависит от того, когда и каким образом система пришла в это состояние. Или состояние некоторой системы в настоящий момент времени (при
) и не зависит от того, когда и каким образом система пришла в это состояние. Или состояние некоторой системы в настоящий момент времени (при 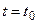 ) однозначно определяет распределение вероятностей будущего развития процесса при
) однозначно определяет распределение вероятностей будущего развития процесса при 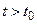 , и информация о прошлом поведении процесса до момента времени
, и информация о прошлом поведении процесса до момента времени 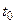 не влияет на это распределение.
не влияет на это распределение.
Замечание. Определяющее марковский процесс свойство называется марковским свойством или свойством отсутствия последействия.
Классификация марковских процессов
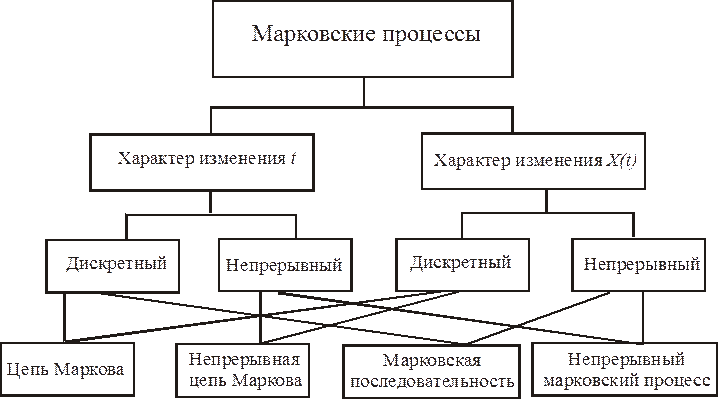
В настоящем курсе будут рассматриваться только марковские процессы с дискретными состояниями (с дискретным характером изменения  , дискретным или непрерывным характером изменения времени
, дискретным или непрерывным характером изменения времени 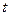 ).
).
Пусть 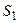 ,
, 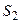 , …,
, …,  - дискретные состояния системы. Марковские процессы с дискретными состояниями удобно иллюстрировать с помощью так называемого графа состояний (см. рис. 4.1), где
- дискретные состояния системы. Марковские процессы с дискретными состояниями удобно иллюстрировать с помощью так называемого графа состояний (см. рис. 4.1), где
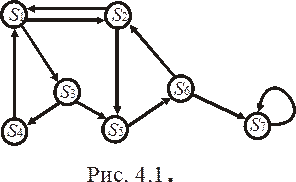 кружками обозначены состояния
кружками обозначены состояния  ,
,  , …,
, …, 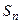 системы;
системы;
стрелками обозначены переходы из состояния в состояние, причём отмечаются только непосредственные переходы из состояния в состояние, а не переходы через другие состояния;
возможные задержки в прежнем состоянии изображают петлёй, т.е. стрелкой, направленной из данного состояния в него же.
Число состояний системы может быть как конечным, так и бесконечным (счётным).
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 388; Нарушение авторских прав?; Мы поможем в написании вашей работы!