Практическое занятие. Марковские процессы

Задания для решения на практическом занятии

1. В процессе эксплуатации ЭВМ может рассматриваться как физическая система 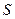, которая в результате проверки может оказаться в одном из следующих состояний: 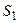– ЭВМ полностью исправна; 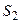– ЭВМ имеет неисправности в оперативной памяти, при которых она может решать задачи, 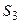– ЭВМ имеет существенные неисправности и может решать ограниченный класс задач; – ЭВМ полностью вышла из строя. В начальный момент времени ЭВМ полностью исправна. Проверка ЭВМ производится в фиксированные моменты времени 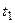, , 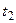. Процесс, протекающий в системе 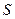, может рассматриваться как однородная марковская цепь с тремя шагами (первая, вторая и третья проверки ЭВМ). Матрица переходных вероятностей имеет вид: . Постройте граф состояний ЭВМ. Определите вероятности состояний ЭВМ после трех проверок.

2. Организация по прокату автомобилей в городе выдаёт автомобили напрокат в трёх пунктах города А, В и С. Клиенты могут возвращать автомобили в любой из трёх пунктов. Анализ процесса возвращения автомобилей из проката в течение года показал, что клиенты возвращают автомобили в пункты А, В, С в соответствии со следующими вероятностями:

Пункты выдачи	Пункты приёма автомобилей
А	В	С
А	0,8	0,2
В	0,2		0,8
С	0,2	0,2	0,6

Требуется:

1) в предположении, что число клиентов в городе не изменяется, найти процентное распределение клиентов, возвращающих автомобили по станциям проката к концу года, если в начале года оно было равномерным;

2) Найти вероятности состояний в установившемся режиме;

3) определить пункт проката, у которого более целесообразно строить станцию по ремонту автомобилей.

3. Водитель такси обнаружил, что если он находится в городе А, то в среднем в 8 случаев из 10 он везёт следующего пассажира в город Б, в остальных случаях будет поездка по городу А. Если же он находится в городе Б, то в среднем в 4 случаях из 10 он везёт следующего пассажира в город А, в остальных случаях будет поездка по городу Б. Требуется:

1) перечислить возможные состояния процесса и построить граф состояний;

2) записать матрицу переходных вероятностей;

3) найти вероятности состояний после двух шагов процесса, если:

а) в начальном состоянии водитель находился в городе А;

б) в начальном состоянии водитель находился в городе Б;

4) найти вероятности состояний в установившемся режиме.

Задания для самостоятельной работы

1. В процессе эксплуатации ЭВМ может рассматриваться как физическая система 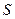, которая в результате проверки может оказаться в одном из следующих состояний: 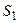– ЭВМ полностью исправна; 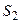– ЭВМ имеет незначительные неисправности, которые позволяют эксплуатировать ЭВМ, 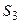– ЭВМ имеет существенные неисправности, дающие возможность решать ограниченное число задач; – ЭВМ полностью вышла из строя. В начальный момент времени ЭВМ полностью исправна. Матрица переходных вероятностей имеет вид: . Постройте граф состояний. Найдите вероятности состояний ЭВМ после одного, двух, трёх осмотров, если в начале (при 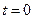) ЭВМ была полностью исправна.

2. Магазин продаёт две марки автомобилей А и В. Опыт эксплуатации этих марок автомобилей свидетельствует о том, что для них имеют различные матрицы переходных вероятностей, соответствующие состояниям «работает хорошо» (состояние 1) и «требует ремонта» (состояние 2): автомобиль марки А 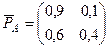, автомобиль марки В . Элементы матриц перехода определены на годовой период эксплуатации автомобиля. Требуется: 1) найти вероятности состояний для каждой марки автомобиля после двухлетней эксплуатации, если в начальном состоянии автомобиль «работает хорошо»; 2) определить марку автомобиля, являющуюся более предпочтительной для приобретения в личное пользование.

3. Система S автомобиль может находиться в одном из пяти возможных состояний: «исправен, работает», «неисправен, ожидает осмотра», «осматривается», «ремонтируется», «списывается». Постройте граф состояний системы.

4. техническое устройство имеет 2 возможных состояния: 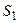– «исправно, работает», 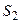– «неисправно, ремонтируется». Матрица переходных вероятностей имеет вид . Постройте граф состояний. Найдите вероятности состояний после третьего шага и в установившемся режиме, если в начальном состоянии техническое устройство исправно.

5. Техническое устройство состоит из двух узлов и может находиться в одном из следующих состояний: оба узла исправны, работают; неисправен только первый узел, неисправен только второй узел, неисправны оба узла. вероятность выхода из строя после месячной эксплуатации для первого узла 0,4; для второго узла – 0,3; вероятность совместного выхода их из строя 0,1. В исходном состоянии оба узла исправны, работают. Запишите матрицу переходных вероятностей и найдите вероятности состояний после двухмесячной эксплуатации.

Тема 5. ЭЛЕМЕНТЫ ТЕОРИИ СИСТЕМ
МАССОВОГО ОБСЛУЖИВАНИЯ

Дата добавления: 2014-01-14