
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
I.I. Метод прогонки
|
|
|
|
Метод прогонки представляет собой частный случай метода исключения Гаусса, ориентированный на специальные системы линейных алгебраических уравнений с ленточной структурой матрицы коэффициентов. А именно, на системы трехточечных уравнений:

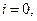

 (1)
(1)
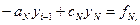

Здесь 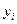 и
и  - компоненты вектора неизвестных и вектора правых частей, а
- компоненты вектора неизвестных и вектора правых частей, а  ,
, 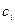 ,
,  образуют трехдиагональную матрицу системы. Формулы метода прогонки для нахождения неизвестных
образуют трехдиагональную матрицу системы. Формулы метода прогонки для нахождения неизвестных 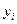 и прогоночных коэффициентов
и прогоночных коэффициентов 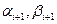 имеют вид /13/
имеют вид /13/
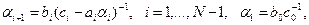

 (2)
(2)

Типичным примером применения метода, прогонки служит численное решение одномерных, нестационарных, линейных уравнений в частных производных. В этой связи рассмотрим первую краевую задачу для уравнения теплопроводности с постоянными коэффициентами
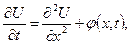 0<
0< <1, 0<
<1, 0<
 (3)
(3)
с соответствующими начальными и краевыми условиями
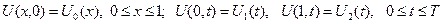 (4)
(4)
Для отыскания приближенного решения y задачи (3), (4) на равномерной сетке  ,где
,где
hи τ шаги сетки по пространственной x и временной t координате, используется однопараметрическое семейство разностных схем (схема с весами)
 (5)
(5)
Здесь вес σ - произвольный вещественный параметр, а разностный оператор Λ является оператором второй разностной производной 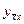 т.е.
т.е. 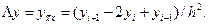
Кроме этого вводится разностный аналог краевых и начальных условий
 (6)
(6)
Решение разностной краевой задачи (5), (6) состоит в определении на каждом n -м временном слое (n=1,..., n0) значений сеточной функции yni с помощью метода прогонки (2). С этой целью соотношения (5), (6) представляются в виде (I). Будем иметь

 (7)
(7)
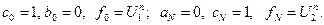
Порядок вычислений формул (2) на одном временном слое отразим граф-схемой (рис.1), вершины которой означают оператор вычисления соответствующей величины, а дуги - отношение предшествования. Найденное решение 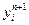 схемы (5) является начальным условием для следующего временного слоя, что отражено на рис.1 дутой из y в f. Кроме того, если коэффициенты разностной схемы не зависят от времени, что, как правило, выполняется при решении линейных задач, то прогоночный коэффициент αi вычисляется один раз вне временного цикла. В соответствии с этим типичным случаем вычисление αi; на рис.1 не показано. Вычисление прогоночного коэффициента βi можно осуществлять по рекуррентной формуле, аналогичной формуле для сеточной функции y, βi+1=pi βi+qi, где
схемы (5) является начальным условием для следующего временного слоя, что отражено на рис.1 дутой из y в f. Кроме того, если коэффициенты разностной схемы не зависят от времени, что, как правило, выполняется при решении линейных задач, то прогоночный коэффициент αi вычисляется один раз вне временного цикла. В соответствии с этим типичным случаем вычисление αi; на рис.1 не показано. Вычисление прогоночного коэффициента βi можно осуществлять по рекуррентной формуле, аналогичной формуле для сеточной функции y, βi+1=pi βi+qi, где
 (8)
(8)
Таким образом, на каждом временном слое по методу прогонки (2) требуется вычислять по N значений βi, yi в соответствии с рекуррентными формулами первого порядка, имеющими чисто последовательный характер выполнения, на каждом шаге которого требуется одно умножение и одно сложение. Если время выполнения этих двух операций, включая также чтение операндов и запись результатов в память, обозначить через 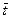 , то время вычисления на одном временном слое сеточных функций βi, yi составит значение 2N
, то время вычисления на одном временном слое сеточных функций βi, yi составит значение 2N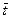 . Кроме того, на каждом временном слое необходимо вычислять величину qi, (см.формулу (8)), что потребует умножения значения
. Кроме того, на каждом временном слое необходимо вычислять величину qi, (см.формулу (8)), что потребует умножения значения  на величину fi, для вычисления которой в соответствии с формулами (7) потребуется дополнительно два умножения, два вычитания и три сложения* плюс время t1, расчета значения
на величину fi, для вычисления которой в соответствии с формулами (7) потребуется дополнительно два умножения, два вычитания и три сложения* плюс время t1, расчета значения  , т.е. всего для вычисления значения fi необходимо время
, т.е. всего для вычисления значения fi необходимо время  где t2 -время выполнения двух вычитаний.
где t2 -время выполнения двух вычитаний.
*Величины в формуле для fi, не зависящие от индекса n, представлены своими значениями, вычисляемыми однократно вне временного цикла.
Последовательный характер вычислений значений yi, входящих в выражение для fi, обуславливают последовательное вычисление N-1 значений qi.. Таким образом, формулы последовательной прогонки (2) реализуются на одном процессоре, и время вычислений на одном временном слое составит значение  .
.
Возможности реализации формул (2) более чем на одном процессоре без применения каких-либо методик распараллеливания весьма ограничены. Исследуем их в случае чисто неявной разностной схемы (σ=1) и в предположении, что правая часть φ не зависит от времени. Тогда по формулам (7), (8) имеем  , где
, где  и значения μi, νi вычисляются вне временного цикла, т.е.
и значения μi, νi вычисляются вне временного цикла, т.е.  .
.
В этом случае для уменьшения значения  можно предложить совмещение расчета значений yi для данного временного слоя и значений qi для следующего временного слоя с помощью двух процессоров в соответствии с диаграммой работы процессоров на рис.2, где цифры на оси абсцисс означают индекс вычисляемой величины, и над соответствующим импульсом проставлен номер временного слоя.
можно предложить совмещение расчета значений yi для данного временного слоя и значений qi для следующего временного слоя с помощью двух процессоров в соответствии с диаграммой работы процессоров на рис.2, где цифры на оси абсцисс означают индекс вычисляемой величины, и над соответствующим импульсом проставлен номер временного слоя.
Так как вычисление значений qi полностью совмещаются с вычислением значений yi, то время расчета на одном временном слое составит здесь величину 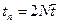 .
.
Формулы (2) определяют правую прогонку (функция yi находится последовательно, начиная от правой границы). Аналогично определяются формулы левой прогонки /13/

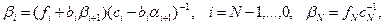 (9)
(9)
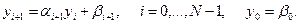
Используя формулы (9) можно совместить расчеты всех трех сеточных функций yi, βi, qi с помощью трех процессоров. Для этого следует чередовать формулы правой (2) и левой (9) прогонки на соседних временных слоях. Пусть первый процессор вычисляет значения yi например, правой прогонкой. По мере появления второй процессор вычисляет значения qi для следующего временного слоя. Это позволяет третьему процессору вычислять по формулам левой прогонки значения βi для следующего временного слоя, на котором наоборот первый процессор осуществляет левую, а третий - правую прогонку. По аналогии с рис. 2 на рис. 3 показана диаграмма работы процессоров. Из диаграммы заключаем, что время вычислений на одном временном слое составляет величину 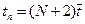 .
.
Комбинацией правой и левой прогонок на одном временном слое является метод встречных прогонок /13/.В этом методе выбирается некоторый m -й узел сетки  и решение в первых m узлах определяется правой прогонкой (2), в последних N-m узлах - левой прогонкой (9), а в m- музле по формуле, содержащей коэффициенты αm, βm (полученные при вычислении соотношений (2) и (9)) и требующей времени примерно
и решение в первых m узлах определяется правой прогонкой (2), в последних N-m узлах - левой прогонкой (9), а в m- музле по формуле, содержащей коэффициенты αm, βm (полученные при вычислении соотношений (2) и (9)) и требующей времени примерно  . Понятно, что допустима одновременная работа двух процессоров. Для обеспечения их более равномерной, загрузки следует выбирать
. Понятно, что допустима одновременная работа двух процессоров. Для обеспечения их более равномерной, загрузки следует выбирать  где развернутые квадратные скобки означают округление до целого с избытком. Процессоры работают одновременно, поэтому с учетом времени
где развернутые квадратные скобки означают округление до целого с избытком. Процессоры работают одновременно, поэтому с учетом времени  для вычисления ym легко установить значение совокупного времени работы на одном временном слое
для вычисления ym легко установить значение совокупного времени работы на одном временном слое  . Здесь квадратные скобки означают округление до целого с недостатком. В соответствии с диаграммой на рис. 2 из этого времени можно исключить время расчета значений qi, выполняя его с помощью двух дополнительных процессоров. Время работы четырех процессоров на одном временном слое составит
. Здесь квадратные скобки означают округление до целого с недостатком. В соответствии с диаграммой на рис. 2 из этого времени можно исключить время расчета значений qi, выполняя его с помощью двух дополнительных процессоров. Время работы четырех процессоров на одном временном слое составит  что равно или всего лишь на
что равно или всего лишь на 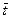 меньше времени работы трех процессоров при чередовании правой и левой прогонки на соседних временных слоях.
меньше времени работы трех процессоров при чередовании правой и левой прогонки на соседних временных слоях.
Результаты анализа алгоритма последовательной прогонки сведем в табл.1. Кроме полученных значений времени и числа процессоров в табл.1 приведены также очевидные значения (приближенные для всех колонок кроме первой) ускорения и эффективности.
Из приведенных результатов ясно, что не удается получить сколь-нибудь заметный эффект параллельной организации вычислений при использовании процедуры последовательной прогонки для решения одномерных уравнений в частных производных. В этой связи рассмотрим применение процедуры последовательной прогонки для решения многомерных краевых задач, в частности, плоских задач.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 1592; Нарушение авторских прав?; Мы поможем в написании вашей работы!