Неявный метод переменных направлений

В литературе по методу сеток широко представлены экономичные схемы решения многомерных уравнений математической физики. Они требуют на каждом временном слое количества операций, пропорционального числу узлов сетки, что обеспечивается использованием процедуры последовательной прогонки для системы p одномерных схем, аппроксимирующих исходное p -мерное уравнение. Этот класс сеточных алгоритмов достаточно широк, но реализация их относительно единообразна, и можно остановиться на таком характерном алгоритме, как неявный метод переменных направлений Писмана-Ракфорда. Пусть p=2. На плоскости Оx₁x₂ введем пространственную квадратную сетку 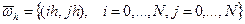что не ограничит общности рассмотрения принципов параллельной реализации метода переменных направлений. Тогда на пространственно-временной сетке ω_hτ схема Писмана-Ракфорда в операторной форме имеет вид /12/

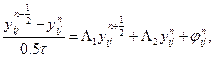(10)

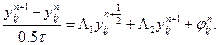(11)

Схема (10), (II) является сеточной аппроксимацией двумерного уравнения теплопроводности. Причем оператор Λ₁ является аппроксимацией дифференциального оператора по направлению x₁, а оператор Λ₂ - по направлению x₂,. В частности, для уравнения теплопроводности с постоянными коэффициентами операторы Λ₁, Λ₂ можно определить выражением второй разностной производной: 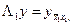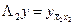.Уравнения (10), (11) являются неявными только по одному из двух направлений x₁, x₂. Т.е. на каждом временном полуслое разностные уравнения относительно искомых величин 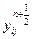или 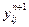- являются трехточечными и могут решаться методом последовательной прогонки (2). Для уравнения теплопроводности с постоянными коэффициентами при решении методом прогонки уравнений (10), (11) коэффициенты a, b, c соответствуют формуле (7) при σ=0.5 а величина f для уравнений (10) и (11) имеет вид

(12)

В случае уравнений с переменными коэффициентами меняются лишь значения величин a, b, c, f в i, j -м узле сетки, что несущественно для нашего анализа метода переменных направлений.

Очевидной возможностью параллельных вычислений для методов типа (10), (11) представляется одновременная обработка всех строк, а затем всех столбцов узлов сетки по формулам прогонки (2). Рассмотрим необходимый при этом межпроцессорный обмен данными для классической MPP системы, содержащей N-1процессорных блоков (ПБ) и блоков памяти (БП), соединенных между собой. Межпроцессорный обмен в такой системе поддерживается линковыми связями точка в точку и общей шиной, как это показано на рис. 4.

Идея одновременной обработки информации для всех строк, а затем для всех столбцов узлов сетки иллюстрируется на рис.5 и реализуется в таком многопроцессорном вычислителе следующим образом. При вычислении сеточной функции 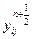ПБ j последовательно обрабатывает информацию по узлам j -й строки сетки. В соответствующем ему БП j имеются необходимые массивы коэффициентов и массив значений сеточной функции 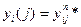хранящий решение на предыдущем полуслое. Во всех ПБ j одновременно вычисляются значения q_i(j) (см.формулу (8)). При этом в соответствии со структурой формулы (12) для f при вычислении величины 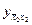в ПБ j, необходимы также значения 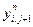и 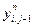, которыми располагают соседние блоки ПБ j±1.

*Индексом обозначен номер элемента массива, целочисленный аргумент в круглых скобках означает номер БП.

Необходимый обмен данными обеспечивается непосредственными двусторонними связями между соседними ПБ (см. рис.4), что технически легко реализуемо и выполняется параллельно для всех ПБ. Далее все ПБ j вычисляют и передают в БП j значения прогоночного коэффициента 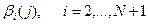и решения 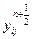, i=N-1,…,0.

При этом одновременно образуются все значения 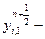в узлах i -го столбца сетки, которые для последующего вычисления в этих узлах значений 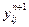с помощью ПБ i должны быть переданы в БП i - так, чтобы 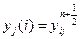и можно было бы одновременно для всех столбцов узлов сетки вычислять в ПБ i новые значения q_j(i), j=1,…,N-1; β_j(i), j=2,…,N+1; 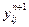, j=N-1,…,0. Аналогично для перехода к следующему временному слою должны быть выполнены пересылки 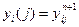параллельно вычисляемых значений .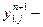

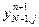Таким образом, на каждую параллельно выполняемую всеми ПБ операцию расчета значений сеточной функции y приходится N-1 операций обмена данными, которые выполняются последовательно, что может свести на нет эффект ускорения решения на параллельной вычислительной системе. Последовательный обмен данными между БП можно исключить благодаря конвейерной организации вычислительного процесса на первом полуслое каждого временного слоя.

При этом в соответствии с рис. 6, обозначения которого аналогичны рис. 5, вычисление значений q, β, y производится по узлам j -й, строки сетки не одним ПБ j, а всеми ПБ так, что, например, значение 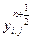вычисляется в ПБ i, который передает это значение в ПБ i-1, а также в БП i и на следующем шаге работы считывает из БП i данные для вычисления значения 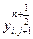в i- музле следующей j+1 -й строки. Таким образом, процессоры "перемещаются" по узлам сетки перпендикулярно направлениям расчета величин β, y и включаются в работу поочередно по мере вычисления этих величин, начиная с ПБ₁ при расчете значений β и с ПБ_N при расчете решения y, что отражено на рис. 6 сдвигом в расположении ПБ по узлам сетки. Обмен данными здесь осуществляется без особых временных затрат с помощью непосредственных связей, соединяющих ПБ _i и ПБ _i±1 (см. рис. 4). Простой ПБ имеет место лишь в силу поочередного включения ПБ в работу и составляет время N-1 расчетов величин β, y т.е. всего 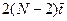, где 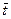время выполнения умножения и сложения и 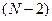обменов ПБ _i±1, т.е. 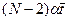После включения последнего ПБ потребуется еще время для N расчетов величины β в узлах N- гостолбца сетки, величины y в узлах первого столбца, т.е. всего 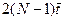. Кроме того, перед вычислением β вычисляются значения q. Этот расчет можно производить синхронно для всех узлов каждой строки в соответствии с организацией параллельных вычислений на рис.5,б, что потребует времени 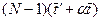. Таким образом, суммарное время работы на первом полуслое составит 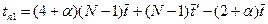. По окончании работы в БП i накопятся значения y по узлам i- гостолбца сетки, и на втором полуслое все ПБ работают параллельно в соответствии с рис.5,б. Время работы очевидно составит Суммарное время метода переменных направлений на одном временном слое для данного алгоритма конвейерной обработки строк, параллельной обработки столбцов (КСПС, рис.6, рис.5,б) определится формулой 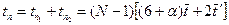. Время однопроцессорной реализации метода на одном временном слое равно времени 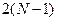прогонок, каждая длительностью 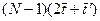, т.е. 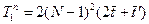. Если правая часть 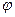не зависит от n то 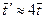. Отсюда , ,

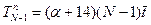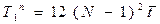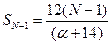
Дата добавления: 2014-01-14