Правила дифференцирования

Теорема 1. Производная постоянной равна 0.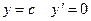

следовательно

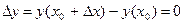
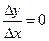
Теорема 2. Постоянный множитель можно выносить за знак производной .

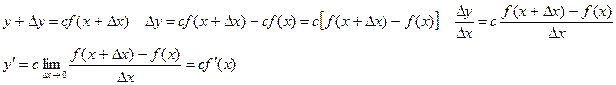
Теорема 3. Производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций

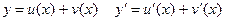
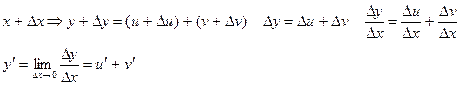
Теорема 4. Производная от произведения двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение производной второй функции на первую

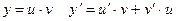
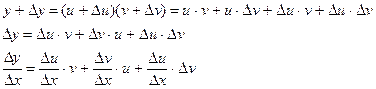
, т.к. функция u дифференцируема, то u^| конечное число, т.к. функция v дифференцируема, то она непрерывна, т.е. 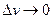при 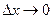Дv – б.м.

Теорема 5. Производная частного двух дифференцируемых функций равна дроби, у которой знаменатель равен квадрату знаменателя, а числитель есть разность произведений производной числителя на знаменатель и производной знаменателя на числитель.

Теорема 6. Производная сложной функции.

Пусть y=F(u) U=ц(x)

y=F(ц(x))

Если U=ц(x) имеет в некоторой точке x производную 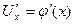, а функция F(U) имеет при соответствующем значении U производную , то сложная функция y=F(ц(x)) в указанной точке x также имеет производную, которая равна 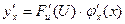, где вместо U должно быть подставлено выражение U=ц(x).

При определенном значении x имеем U=ц(x) y=F(U) при аргументе x+Дx 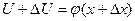; 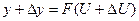, при 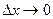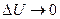, а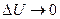 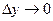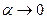при . , при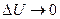

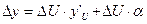
Разделим на 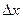: . . 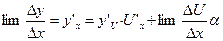, т.к. 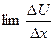- конечное число.

Дата добавления: 2014-01-14