Решение и геометрическая интерпретация игры (2x2)

.

Если платёжная матрица игры обладает свойством, то такая игра называется с седловой точкой. На платёжной матрице такой игры существует элемент

Во втором примере. Анализ игры показал, что наилучшими стратегиями будут чистые стратегии.

В первом примере, и мы убедились при анализе этой игры, что наилучшие стратегии игроков будут смешанные стратегии.

Этот элемент называется седловой точкой, для которой справедливо неравенство

.

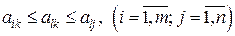Величина 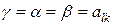называется чистой ценой игры. Пара стратегий 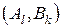является оптимальной парой, то есть образует решение игры 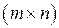среди чистых стратегий.

Теорема. Любая конечная парная игра с нулевой суммой и с полной информацией является игрой с седловой точкой.

Например, игры в шашки, шахматы являются конечными, парными играми с нулевой суммой и с полной информацией, поэтому они относятся к играм с седловой точкой.

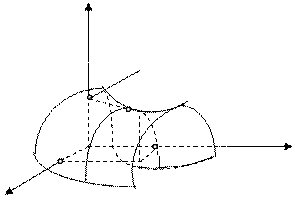
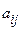
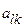
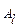
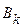
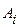
Графическая интерпретация игры с седловой точкой представлена на рисунке. Если игрок 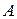допускает отклонение от своей оптимальной стратегии 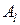, то он ухудшает свое положение, скатываясь по разрезу седла. Аналогично для игрока 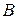, он будет увеличивать выигрыш игрока 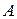, поднимаясь по профилю седла.

В теории игр доказывается, что каждая игра с полной информацией имеет седловую точку и следовательно, решение в чистых стратегиях. Другими словами, в каждой игре с полной информацией существует пара оптимальных стратегий той и другой стороны, дающая устойчивый выигрыш, равный чистой цене игры. Если игра с полной информацией состоит только из личных ходов, то при применении каждой стороной своей оптимальной стратегии игра должна кончаться всегда вполне определенным исходом, равным цене игры.

В качестве примера приведем следующую игру с полной информацией. Два игрока поочередно кладут одинаковые монеты на круглый стол, выбирая произвольно положение монеты (взаимное перекрытие монет не допускается). Выигрывает тот, кто положит последнюю монету (когда места для других уже не останется). Нетрудно убедиться, что исход этой игры предрешен, и существует определенная стратегия, обеспечивающая достоверный выигрыш тому из игроков, кто кладет монету первым. А именно, он должен первый раз положить монету в центр стола, а далее на каждый ход противника отвечать симметричным ходом. Очевидно, как бы ни вел себя противник, ему не избежать проигрыша. Поэтому игра имеет смысл только для лиц, не знающих ее решения. Точно так же дело обстоит с шахматами и другими играми с полной информацией; любая из этих игр обладает седловой точкой и, значит, решением, указывающим каждому игроку его оптимальную стратегию, так что игра имеет смысл только до тех пор, пока неизвестно решение. Решение шахматной игры не найдено (и в обозримом будущем вряд ли будет найдено) только потому, что число стратегий (комбинаций ходов) в шахматах слишком велико, чтобы можно было построить платежную матрицу и найти в ней седловую точку.

Если игра (2х2) имеет седловую точку, то ее решение очевидно. Пусть игра без седловой точки с платежной матрицей (a_ij)_2x2. Требуется найти оптимальные смешанные стратегии игроков 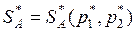и 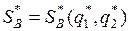и цену игры g. В игре (2х2) без седловой точки обе стратегии игроков являются активными. Поэтому в соответствии с теоремой об активных стратегиях, если игрок А будет применять свою оптимальную смешанную стратегию, то независимо от действия игрока В, выигрыш его будет равен цене игры g.

Пусть игрок А использует стратегию 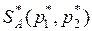, а игрок В – стратегию В₁. Тогда выигрыш игрока А определяется из уравнения

.

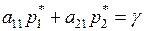Если же игрок В будет применять стратегию В₂, то выигрыш игрока А не изменится и будет определяться равенством

.

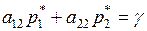Принимая во внимание условие 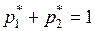, можно записать систему уравнений с тремя неизвестными величинами:

,

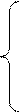
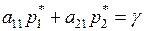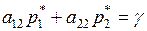, (1)

.

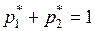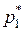Решив эту систему уравнений, находим оптимальную смешанную стратегию игрока А, т.е. и .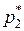

Аналогично определяется оптимальная стратегия 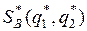игрока В из системы уравнений:

,

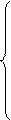
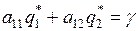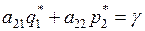, (2)

.

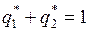В результате решения системы уравнений (2) находятся вероятност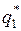и и 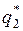, т.е. оптимальная стратегия .

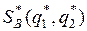Игра (2х2) допускает простую геометрическую интерпретацию. Для этого в системе координат хОу на оси абсцисс откладывается отрезок [А₁,А₂], равный единице, и через концы этого отрезка проводятся перпендикулярные к оси абсцисс прямые, на которых откладываются выигрыши игрока А (рис.1).

Левый перпендикуляр, совпадающий с осью ординат, соответствует стратегии А₁, для которой Р₁=1, Р₂=0, а правый равен стратегии А₂, для которой Р₁=0, Р₂=1. При применении игроком В стратегии В₁ выигрыш будет а₁₁, если игрок А использует стратегию А₁, и будет а₂₁, если он применяет стратегию А₂. Отложив отрезки, равные а₁₁ и а₂₁ на соответствующих перпендикулярах получим две точки: В₁ соответствующий стратегии А₁ и В₁ соответствующий стратегии А₂. Ордината любой точки отрезка В₁В₂ равна величине выигрыша игрока А при применении им стратегии А₁ и А₂ с вероятностями Р₁ и Р₂.

Если игрок В применяет стратегию В₂, то выигрыш игрока А равен а₁₂ при использовании стратегии А₁, и а₂₂ – стратегии А₂. Ординаты точек, лежащие на отрезке В₂В₂, равны среднему выигрышу игрока А, если он применяет стратегии А₁ и А₂ с вероятностями Р₁ и Р₂, а противник -–стратегию В₂.

Для нахождения оптимальной стратегии построим нижнюю границу выигрыша игрока А, т.е. ломаную В₂NB₁, отмеченную на рис.1 линией. Очевидно, что на этой ломанной лежат минимальные выигрыши игрока А при использовании им любой смешанной стратегии.

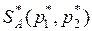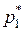Оптимальное решение игры определяет точка N, в которой выигрыш игрока А принимает наибольшее значение (проигрыш игрока В наименьшее значение) равный цене игры g. Проекция этой точки на ось абсцисс соответствует оптимальной стратегии , при этом расстояния от точки до концов единичного отрезка на оси абсцисс равны вероятностям и .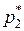

Оптимальная стратегия 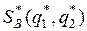игрока В находится аналогично. Для этого необходимо поменять местами игроков А и В. (см. рис.2)

На рис.1 и 2 решение игры определялось точкой пересечения стратегий, однако это справедливо не всегда. Так, например на рис.3 показан случай, когда нижняя граница выигрыша игрока А совпадает с отрезком В₂В₂, т.е. стратегия В₁ для игрока В заведомо не выгодная. Здесь 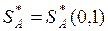, игра имеет седловую точку.

На рис.4 показан случай, в котором 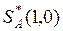,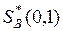. Игра имеет седловую точку.

Дата добавления: 2014-01-14