Приближенное решение дифференциальных уравнений

Класс уравнений, для которых можно получить точное решение, то есть, аналитическую функцию, удовлетворяющую заданному дифференциальному уравнению и всем дополнительным условиям (задача Коши), очень узок. Чаще всего дифференциальные уравнения решаются приближенно. С одним из методов – итерационным – мы познакомились при доказательстве теоремы существования и единственности.

1. Приближение решения с помощью степенного ряда. Представим, что мы должны решить задачу Коши для дифференциального уравнения -го порядка 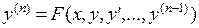с начальным условием 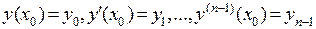. Если функция в правой части уравнения разлагается в ряды по всем своим переменным, удобно искать решение дифференциального уравнения в окрестности точки 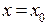в виде ряда Тейлора по степеням 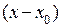. Представим решение в виде 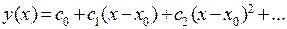. Из начальных условий и свойств коэффициентов ряда Тейлора следует, что все коэффициенты разложения вплоть до 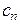нам известны:

остальные – неизвестные – коэффициенты обозначаются буквами и определяются сравнением коэффициентов при одинаковых степенях, находящихся в обеих частях дифференциального уравнения.

П р и м е р. Решить следующую задачу Коши: , .

Искать решение будем в виде ряда по степеням 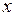. В соответствии с начальными условиями . Подставим хотя бы первые слагаемые рядов в уравнение:

Перемножим входящие в правую часть сомножители:

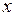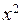А теперь сравним свободные члены (они равны) и коэффициенты при , при и при : 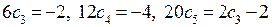. Отсюда .

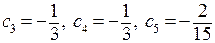Мы могли бы и далее сравнивать коэффициенты при степенях 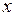в уравнении и получать значения других коэффициентов . Тем более применение программ MAXIMA упрощает этот процесс. В данном случае мы получили решение в виде ряда, первые члены которого известны: .

Задачу Коши для системы уравнений можно решать подобным способом.

2. Метод Эйлера и его модификации. Познакомимся с методом Эйлера численного решения задачи Коши для дифференциального уравнения первого порядка 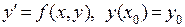. Предположим, что мы должны решить задачу на отрезке 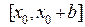. Разделим отрезок 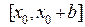на равных частей, равных . Заменим на каждом отрезке , , решение дифференциального уравнения линейной функцией 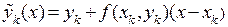. При этом имеем узловые значения решения: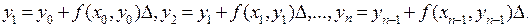

Мы здесь приравниваем отношение приращений функции и аргумента производной в точке, соответствующей началу отрезка разбиения:

.

Очевидно, что такое приближение является тем менее точным, чем дальше мы отойдем от точки 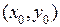. Метод Эйлера является наиболее примитивным. Здесь интегральная кривая заменяется ломаной, состоящей из прямолинейных отрезков. Возможны его некоторые модификации, несколько улучшающие точность. Например, если брать постоянные значения в виде

.

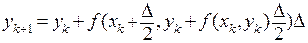Наиболее распространенным численным методом решения указанной задачи Коши является метод Рунге-Кутта. При решениидифференциального уравнения этим методом интегральная кривая заменяется ломаной, состоящей из кусков парабол. Метод Рунге-Кутта встроен в пакет программ MAXIMA.

Например, мы хотим решить дифференциальное уравнение с начальным условием 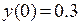. При этом мы задаем отрезок [0,1], на котором хотим получить численное решение и шаг разбиения этого отрезка, равный 0.05. Мы должны ввести команду

load(dynamics); rk(y^2+x,y,0.3,[x,0,1,0.05]);

После того, как мы нажмем клавиши Shift+Enter, получим данные

[[0,0.3],[0.05,0.30583128660202],[0.1,0.31438277172198],[0.15,

0.32574776902574],[0.2,0.34003114365951],[0.25,0.35735268712942],[0.3,

0.37785103897622],[0.35,0.40168830090343],[0.4,0.42905553899765],[0.45,

0.46017943684494],[0.5,0.49533045405802],[0.55,0.53483297195895],[0.6,

0.57907808748734],[0.65,0.62853997325452],[0.7,0.6837970957275],[0.75,

0.74556013793749],[0.8,0.81470931041585],[0.85,0.89234502470182],[0.9,

0.97985793824278],[0.95,1.079027666994073],[1.0,1.192164923146931]].

Это означает, что мы получили узловые значения решения: y (0.05)= 0.30583128660202,…, y (0.4)= 0.42905553899765,…..

Приближенное решение дифференциальных уравнений высших порядков сводятся к решению систем уравнений первого порядка. Например, требуется решить дифференциальное уравнение 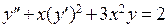на отрезке [0,2] с шагом 0.1 при начальных условиях 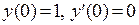. Введем новую функцию . Теперь уравнение запишется в виде системы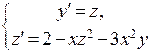

с начальными условиями .

Для получения решения методом Рунге-Кутта вводим команду load(dynamics); rk([z,2-x*z^2-3*x^2*y], [y,z], [1,0], [x,0,2,0.1]).

Мы получим значения в узлах:

[[0,1,0],[0.1,1.009973277486667,0.19889443755825],[0.2,1.03953179049664,

0.39025908431976],[0.3,1.087443707860848,0.56407930484999],[0.4,1.151355476824082,

0.70808296273707],[0.5,1.227625229955781,0.80905909503231],[0.6,1.31132100772257,

0.85473889531278],[0.7,1.396404177611673,0.83546996450053],[0.8,1.476033430956961,

0.74483368487679],[0.9,1.542855824183935,0.57873490276185],[1.0,1.589128945076604,

0.33294944409803],[1.1,1.606518986789783,-9.8829227227875682*10^-4],[1.2,

1.585353126452777,-0.44308261198787],[1.3,1.512758668789601,-1.041803224981043],[1.4

,1.367721332806764,-1.927748829187044],[1.5,1.104119674291387,-3.562685524381777],[

1.6,0.55276102463945,-9.157645341403534],[1.7,-3.785389000081017,-789.9052329768924],

[1.8,-1.8741633219283803*10^14,-3.7934868677108632*10^30]].

Это означает, что, например, y(0.5)= 1.227625229955781,

z(0.5)= 0.80905909503231.

3. Графический метод. Этим методом можно решать дифференциальные уравнения первого порядка вида . Если нам необходимо построить интегральные кривые, которые являются графиками решений приведенного уравнения, в какой-то части плоскости 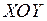, мы каждой точке 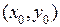этой области ставим в соответствие значение , которое совпадает с тангенсом угла наклона касательной к интегральной кривой, проходящей через точку 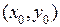. Зная точку и направление движения по кривой из этой точки, мы переходим к близкой точке, в которой также определяем направление движения,…. Так, двигаясь от точки к точке, мы построим соответствующую интегральную кривую, то есть, решим задачу Коши .

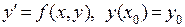Реальное построение решения таким методом было бы очень сложным без применения компьютерной техники. MAXIMA содержит программу построения графических решений. Если мы введем load(plotdf); plotdf(f(x,y),[y,c,d],[x,a,b]), на экране появится прямоугольник , в точках которого указаны направления касательных к интегральным кривым, проходящим через эти точки. Если щелкнуть курсором по выбранной точке на плоскости, компьютер нарисует интегральную кривую, проходящую через соответствующую точку.

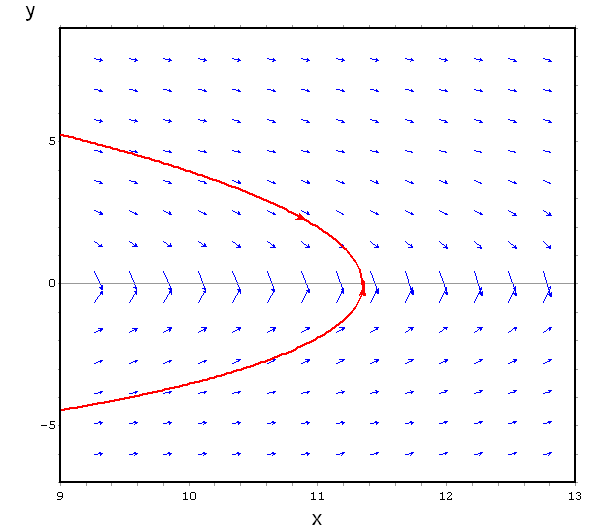
Например, мы хотим построить интегральную кривую уравнения , расположенную в прямоугольнике 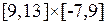и проходящую через точку (11,2).

Введем load(plotdf); plotdf((5-x^2)/(2*x*y-y^2),[y,-7,9],[x,9,13]); и нажмем Shift+Enter. Мы получим выбранный прямоугольник с указанием направлений из точек прямоугольника. Теперь щелкнем по точке (11,2), и нарисуется соответствующая интегральная кривая.

Дата добавления: 2014-01-14