Специальные вопросы изгиба

12.1. Оптимизация элементов конструкций. Общие понятия

Под оптимальным проектированием принято понимать такое назначение характеристик конструкции, несущей нагрузки, при котором она в определенном смысле будет наилучшей из всех конструкций рассматриваемого типа.

Признаки, используемые при оптимизации, называются критериями оптимизации. Критерий оптимизации – это величина, которая в ходе поиска оптимального решения должна принять либо минимум, либо максимум. После того как определена цель проектирования и выбраны критерии оптимизации, формируется целевая функция – функция, включающая в себя все критерии и их вклад (важность) в искомое решение, затем разрабатываются модель и метод оптимизации, с помощью которых ищется максимум или минимум целевой функции.

При решении оптимизационных задач приходится принимать во внимание очень многие факторы, учесть которые удается только при помощи ЭВМ с использованием специальных методов.

Далее мы рассмотрим элементарные примеры оптимального проектирования

конструкций при изгибе.

Как правило, в сопротивлении материалов за критерий оптимизации принимают или минимальный вес конструкции или максимальную нагрузку, которую может выдержать элемент. При этом очень часто критерий минимального веса заменяется критерием равнопрочности (то есть равенство напряжений во всех сечениях элемента конструкции).

12.2. Балки равного сопротивления при изгибе

До сих пор мы рассматривали расчет на изгиб стержней, сечение которых оставалось постоянным по длине. Такие стержни, особенно при значительной их длине, нельзя считать рациональными с точки зрения веса и расхода материала, так как размеры сечения подбираются по усилиям, действующим в опасном сечении, в остальных же сечениях получается весьма значительный избыток прочности. Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления, у которых во всех сечениях наибольшее нормальное напряжение одинаково и не превышает допускаемого значения.

Условие, определяющее форму такой балки, получим из условия прочности:

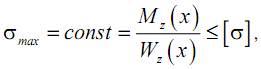
отсюда можем записать

То есть у балки равного сопротивления момент сопротивления данного сечения должен быть прямо пропорционален изгибающему моменту в этом сечении.

Рассмотрим некоторые примеры проектирования балок равного сопротивления.

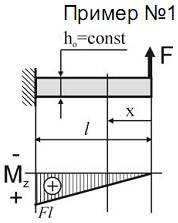Дано:

Рассмотрим консольную балку длиной l прямоугольного сечения постоянной высоты hо и переменной ширины b(x), загруженную силой F.

Определить:

Найти закон изменения ширины сечения балки b(x) из условия равнопрочности.

Решение

Определим закон изменения изгибающего момента и построим его эпюру по длине балки:

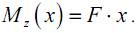
Момент сопротивления прямоугольного сечения в общем виде можем записать как

в нашем же случае

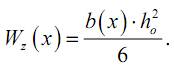
Величину b(x) найдем из условия (12.1):

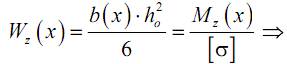
– ширина сечения в опасной точке.

Как видим, ширина балки в данном случае должна изменяться по линейному закону по длине балки.

Дата добавления: 2014-01-14