Пример №2

Дано:

Рассмотрим консольную балку длиной l прямоугольного сечения постоянной ширины bо и переменной высоты h(x), загруженную силой F.

Определить:

Найти закон изменения высоты сечения балки h(x) из условия равнопрочности.

Решение

Определим закон изменения изгибающего момента и построим его эпюру по

длине балки:

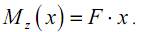
Момент сопротивления прямоугольного сечения в общем виде можем записать как

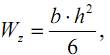
в нашем же случае

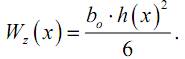
Величину h(x) найдем из условия (12.1):

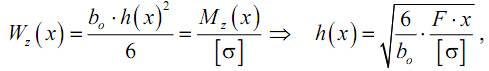
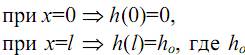– высота сечения в опасной точке.

Как видим, высота балки в данном случае должна изменяться по закону квадратичной параболы по длине балки.

Рассмотренные примеры часто находят применение на практике, например, при проектировании рессор. Рассматривая рессору как балку на двух опорах, легко найти, что брус равного сопротивления будет иметь форму ромба. При этом, так как подобная конструкция крайне неудобна в эксплуатации, поступают следующим образом. Представим, что лист рессоры разделен на узкие полоски. Если расположить эти полоски не рядом друг с другом, а одна над другой, то работа такой балки не изменится, а ее конструкция станет более компактной.

Другим примером использования балок переменного сечения в

машиностроительной практике являются конструкции ступенчатых валов. Здесь, для удобства изготовления и применения такого вала, размеры сечения стержня изменяются по длине вала не плавно, как в предыдущих примерах, а ступенчато. При этом размеры каждой из ступеней вала выбираются, с одной стороны, из конструктивных соображений, а с другой, так, что-бы напряжения в сечениях вала не превышали допускаемых (то есть – из условия прочности).

12.3. Касательные напряжения при изгибе балок тонкостенного профиля

При поперечном изгибе тонкостенного стержня в его сечениях преобладающими остаются нормальные напряжения, которые в основном и определяют прочность стержня. Однако здесь, в отличие от стержня сплошного сечения, существенное значение приобретают касательные напряжения и законы их распределения. Тонкостенные стержни замкнутого профиля сопротивляются нагрузкам примерно также, как и массивные. Иначе обстоит дело с тонкостенным открытым профилем (незамкнутое сечение).

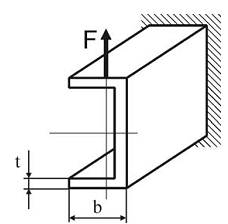Допущения, положенные в основу вывода формулы Журавского для касательных напряжений (формула (10.10), лекция 10), в достаточной степени соответствуют действительности для массивного сечения. Когда сечение представляет собой тонкостенный профиль, например, вроде швеллера, его ширина b значительна (по сравнению с толщиной t) и картина распределения касательных напряжений здесь существенно меняется: они не только переменны вдоль средней линии полки, но и направление их становится не параллельным к поперечной силе Q.

Заметим, что в полках будут действовать и касательные напряжения, параллельные Q. Однако эти напряжения настолько малы, что их можно не принимать во внимание.

Выведем формулу для вычисления касательных напряжений (обозначим их τxz) в полках тонкостенных профилей (на примере швеллера). Учитывая, что полка узкая (t мало по сравнению с b), примем следующие допущения: 1) касательные напряжения τxz постоянны по толщине полки и зависят только от расстояния z до вертикальной оси; 2) всюду в полке касательные напряжения τxz параллельны ее средней линии.

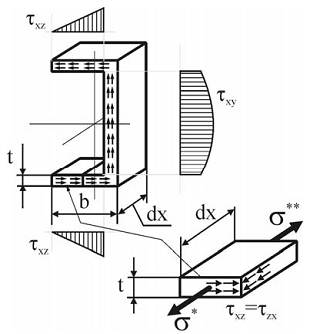Рассматривая равновесие отсеченной части полки (шириной dx) подобно тому, как это делалось при выводе формулы Журавского (формула (10.10), лекция 10), заметим, что на передней и задней гранях элемента возникают нормальные напряжения σ* и σ**

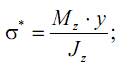
а также касательные напряжения τxz. Точно такие же напряжения τzx будут возникать и на боковой грани элемента (по закону парности касательных напряжений). Остальные поверхности элемента свободны от напряжений, так как являются наружными (незагруженными) поверхностями балки. Проецируя все силы, действующие на элемент, на ось x, получим:

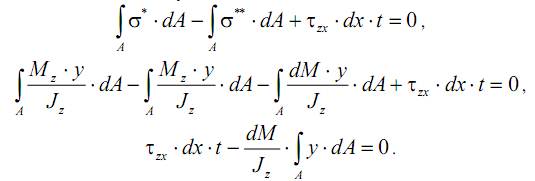
Как видим, вывод формулы для напряжений τxz совершенно аналогичен выводу формулы Журавского для касательных напряжений при поперечном изгибе (см. лекцию 10). Поэтому, не повторяя дальнейших рассуждений, окончательно можем записать

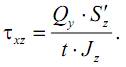
Обобщая изложенное на случай тонкостенного сечения с произвольным незамкнутым криволинейным профилем, можем констатировать, что при изгибе от поперечной

силы Q в сечении возникают касательные напряжения τп, равномерно распределенные по толщине стенки t и ориентированные по касательной к очертанию контура сечения. Определяются эти напряжения по формуле Д. И. Журавского для тонкостенного незамкнутого сечения:

где zS′ – статический момент отсеченной части сечения (на рисунке заштрихована) относительно оси z.

12.4. Понятие о центре изгиба тонкостенных стержней

Как было отмечено выше, касательные напряжения в незамкнутых поперечных сечениях тонкостенных стержней образуют «поток», параллельный к контурным линиям каждого элемента сечения. В некоторых случаях этот поток может создавать момент относительно оси стержня, вызывающий его закручивание и искривление (депланацию) сечения.

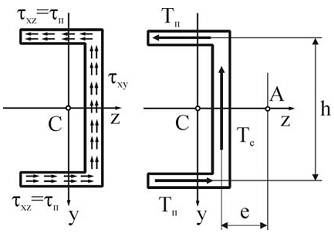Рассмотрим поперечный изгиб консольной балки швеллерного сечения в плоскости x0y. В стенке швеллера будут возникать касательные напряжения τxy, а в полках – касательные напряжения τxz=τп. Равнодействующей касательных напряжений в стенке (τxy) является сила Тс, которая практически равна внутренней поперечной силе Qy (Тс≈Qy). Касательныенапряжения в полках (τxz=τп) приводятся к равнодействующим силам Тп.

Нетрудно видеть, что силы Тс и Тп создают момент относительно центра тяжести швеллера, вызывающий закручивание стержня (помимо его изгиба).

Таким образом, если линия действия внешней силы F проходит через центр тяжести сечения швеллера, то балка будет испытывать изгиб с кручением. Как известно, открытые (незамкнутые) тонкостенные профили плохо работают на кручение. Кроме того, если балка заделана так, что депланация сечения в заделке становится невозможной, то будет иметь место так называемое стесненное кручение, при котором в сечении дополнительно возникают не только касательные, но и значительные нормальные напряжения. Поэтому желательно принимать меры, устраняющие кручение в балках прокатного профиля.

Установим положение такой точки, при прохождении через которую линии действия внешней силы поток касательных напряжений при изгибе не будет вызывать закручивания стержня. Очевидно, что такая точка А расположена на оси 0z вне контура сечения швеллера, поскольку при этом равнодействующие касательных напряжений Тс и Тп будут давать моменты разных знаков относительно точки А. Составим уравнение равновесия сечения швеллера под действием сил Тс и Тп:

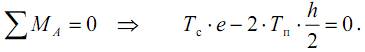
Отсюда находим положение точки А для швеллера:

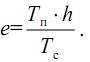
Итак, если линия действия силы F будет проходить через точку А, то стержень будет испытывать только изгиб. Поэтому точка А называется цен тром изгиба, а продольная ось, проходящая через эту точку, – осью центров изгиба.

Ось центров изгиба обладает тем свойством, что поперечная нагрузка, пересекающая эту ось, вызывает только изгиб стержня. В противном случае возникает дополнительная деформация кручения относительно этой оси.

В общем случае центр изгиба не совпадает с центром тяжести сечения, и его положение подлежит определению. В некоторых случаях положение центра изгиба устанавливается без предварительных вычислений. Так, для сечений с двумя осями симметрии, например, для двутавра центр изгиба совпадает с центром тяжести сечения. Это имеет место также для так называемых кососимметричных сечений (например, для показанного на рисунке «зетового» сечения). Для сечений в виде тавра и уголка центр изгиба находится в точке пересечения средних линий элементов сечения (момент касательных напряжений относительно этой точки здесь равен нулю).

Таким образом, наряду с основной продольной осью x, проходящей через центр тяжести сечений, стержень обладает еще осью центров изгиба, к точкам которой должны приводиться поперечные нагрузки при разделении деформаций изгиба и кручения. Иногда эта ось называется осью жесткости, а сама точка А – центром жесткости (центром сдвига).

Дата добавления: 2014-01-14