Свойства эвольвентного зацепления

Зацепление проектируемой поверхности зубьев с производящей поверхностью по аналогии с зацеплением нарезаемого колеса с производящей поверхностью режущего инструмента называют станочным зацеплением.

Геометрические элементы зубчатых колес

Все термины, определения и обозначения стандартизированы и даются по ГОСТ 16530-83 и ГОСТ 16531-83, а расчет геометрии (формулы, порядок расчета) по ГОСТ 16532-70.

В основу измерения многих элементов зубчатых колес принята начальная окружность в станочном зацеплении.

Если производящее колесо (инструмент) имеет конечное число зубьев, то режущим инструментом может быть долбяк. При бесконечно большом количестве зубьев производящего колеса, оно превращается в рейку.

Реечный контур, принятый в качестве базового для определения теоретических форм и размеров зубьев, называют исходным контуром.

Параметры исходного контура также являются стандартными и регламентируются ГОСТом 13755-81.

Начальные окружности, которые являются центроидами в относительном движении двух колес, в станочном зацеплении называются делительными окружностями (делят зуб на головку зуба и на ножку зуба). d – обозначение диаметра делительной окружности (r – радиуса).

Расстояние, измеренное по дуге делительной окружности, вмещающее одну ширину впадины и одну толщину зуба, называется шагом зацепления ( обозначается – p).

πd = pz d = (p/π)z

Если за основу взять шаг зацепления, то точно делительный диаметр посчитать нельзя. Тогда взяли p/π = m. Где m – назвали модулем и приняли за основу стандартизации в метрической системе мер. Модуль по ГОСТ 9563-60 измеряется в мм. Таким образом, d = mz.

Радиальное расстояние от делительной окружности до окружности вершин зубьев называется высотой головки зуба.

Рисунок 4.

дульных колес (m≥1мм) h^*_а = 1, для мелкомодульных колес (m<1мм) h^*_а = 1.

Высотой ножки зуба называется радиальное расстояние от окружности впадин до делительной окружности.

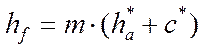
Где с ^* - коэффициент радиального зазора

с ^* = 0,25 для m≥1мм и с ^* =0,35…0,5 для m<1мм

Тогда диаметр вершин зубьев d_a

d_a = d + 2h_a

По некоторым соображениям, о которых мы поговорим позже, заготовку или зуборезную рейку иногда отодвигают друг от друга на величину S= хm, где х – коэффициент смещения.

Тогда 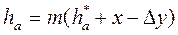, где 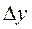- коэффициент уравнительного смещения, который вводится для получения зубчатой передачи без бокового зазора и со стандартной величиной радиального зазора.

Учитывая все ваше приведенное, получим

Это все для колес с внешними зубьями. Для колес с внутренними зубьями выражения следующие

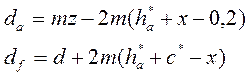
Для того чтобы получать стандартные колеса, стандартизируют параметры зуборезного инструмента (т.е. параметры исходного контура, а именно 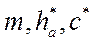и 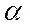), где α = 20⁰ – угол профиля зуба исходного контура (рис.4.).

1. Л.Эйлер доказал, что при эвольвентном зацеплении наименьшее скольжение в точке контакта сопряженных профилей зубьев.

2. Эвольвентное зацепление удовлетворяет основному требованию кинематики – постоянству передаточного отношения.

Действительно, поскольку нормаль в точке контакта к сопряженным профилям зубьев, по свойству эвольвенты, касается обеих основных окружностей, то контакт профилей зубьев всегда происходит на этой нормали. Так как основные окружности при вращении колес не меняют свое относительное положение, то и нормаль всегда пересекает линию межосевого расстояния в одном и том же месте. Это значит, что передаточное отношение за время зацепления одной пары зубьев будет постоянным.

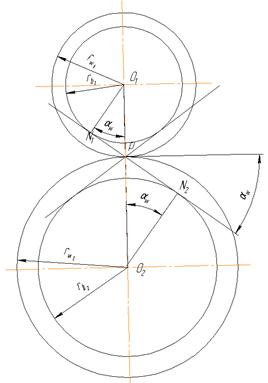Линия, на которой происходит контакт сопряженных профилей зубьев, называется линией зацепления. Из двух ветвей линии зацепления рабочей является та, которая как бы сматывается с основной окружности колеса, связанного с источником энергии и наматывается на основную окружность колеса, связанного с потребителем энергии.

Углом зацепления a_W называется угол, составленный каждой ветвью линии зацепления с перпендикуляром к линии межосевого расстояния. В станочном зацеплении он равен углу a.

3. При передаче постоянного крутящего момента давления на зубья и опоры колес будут постоянны.

Так как давление от одной поверхности зуба к другой (без учета сил трения) передается по нормали, т.е. по линии зацепления, то плечом момента силы будут являться радиусы основных окружностей, которые постоянны. Следовательно, при постоянных моментах на колесах и сила давления на зубья и опоры будет постоянной.

4. Незначительное изменение межосевого расстояния (погрешность изготовления, монтажа и т.д.) не изменяет передаточного отношения пары зубчатых колес.

Из рисунка 6 следует

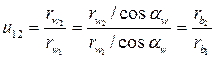
Так как радиусы основных окружностей при изменении межосевого расстояния не меняются, то и передаточное отношения тоже не меняется.

Из этого же рисунка следует

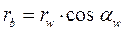
Для станочного зацепления

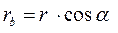
К числу свойств эвольвентного зацепления относится и свойство беззазорного зацепления (отсутствие бокового зазора). Особенно это важно при реверсивном движении.

Из условия беззазорного зацепления и перекатывания начальных окружностей без скольжения можно записать

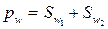
Где 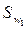и 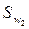-толщина зубьев по начальной окружности колес, а 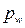- шаг по начальной окружности.

Если толщину зубьев и шаг выразить через число зубьев, коэффициент смещения и угол зацепления, то после преобразования можно получить [1]

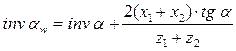
(1)

Из этого условия можно найти угол зацепления, который используется при определении межосевого расстояния.

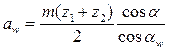(2)

5. Обработка эвольвентных зубчатых колес

5.1. Способы изготовления эвольвентных профилей зубьев зубчатых колес.

Обычно используются два способа обработки и получения эвольвентных профилей. Это способ копирования и способ обкатки (огибания).

При способе копирования боковая поверхность (режущая кромка) инструмента является точной копией боковой поверхности зуба. За один проход инструмента (модульная пальцевая фреза, модульная дисковая фреза) на заготовке нарезается одна впадина. Затем заготовка поворачивается на угловой шаг (с помощью делительной головки) и снова нарезается одна впадина и т.д. Основной недостаток этого метода – наличие нескольких комплектов инструмента для нарезания зубьев одного и того же модуля, так как с изменением числа зубьев на колесе профиль зуба меняется.

Станки и инструменты для нарезания способом копирования:

а) Станок универсально-фрезерный, инструмент – модульная дисковая фреза.

б) Станок консольно-фрезерный, инструмент – модульная пальцевая фреза.

а) Станок протяжный, инструмент – протяжка.

г) Отливка по готовой модели.

Наиболее часто используется способ обкатки, который заключается в том, что инструмент (в виде колеса, рейки и т.д.) вводят в зацепление с еще не изготовленным колесом (заготовкой) и задают им такие относительные движения, как будто колесо изготовлено. При этом инструмент совершает и технологические ходы. В результате такой обкатки происходит нарезание колеса.

Станки и инструменты для нарезания способом обкатки:

а) Станок зубодолбежный, инструмент – долбяк.

б) Станок зубострогальный, инструмент – зуборезная рейка.

в) Станок зубофрезерный, инструмент – модульная червячная фреза.

г) Прокатка зубчатых колес в ковочном состоянии между зубчатыми валками.

5.2.. Явления интерференции, подрезания и заклинивания зубчатых колес.

Дата добавления: 2014-01-14