Интерференция - наложение профиля зуба одного колеса на профиль зуба другого при проектировании зацепления

Подрезание – наложение профиля зуба инструмента на профиль зуба изготавливаемого колеса при нарезании зубьев.

Заклинивание – наложение профилей зубьев, но не при изготовлении, а при зацеплении колес.

Рассмотрим подробней явление подрезания. Так как параметры зуборезного инструмента стандартны, то при прочих равных условиях возможность подрезания ножки зуба определяется положением точки N, т.е. размерами колеса. Подрезание не происходит, когда точка контакта между производящей поверхностью инструмента и профилем зуба нарезаемого колеса находится правее точки N. Левее точки N эти поверхности будут не касаться друг друга, а пересекаться, что и приводит к подрезанию ножки зуба. Подрезание уменьшает эвольвентную часть профиля зуба колеса, ослабляет прочность зуба в опасном сечении и уменьшает коэффициент перекрытия.

Рассмотрим вопрос о наименьшем числе зубьев Z_min на колесе, при котором явление подрезания будут отсутствовать при нарезании зубьев рейкой с учетом смещения.

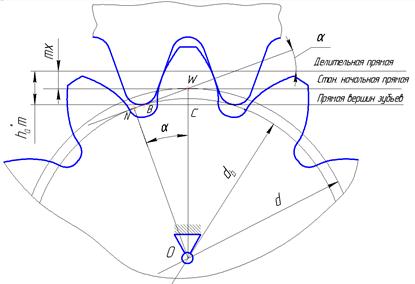По условию не подрезания, должно выполняться условие NW ≥ BW. Из треугольника ОNW можно выразить катет NW, используя модуль и число зубьев

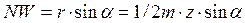
Из треугольника BWC можно найти гипотенузу BW, используя модуль,

высоту головки зуба и коэффициент смещения Рисунок 5 инструмента

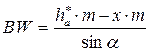
Тогда

≥

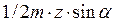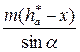
Отсюда число зубьев, которое можно нарезать реечным инструментом без подрезания ножки зуба, с учётом смещения будет равно

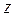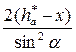= (3)

Минимальное число зубьев без смещения реечного инструмента и без подрезания ножки зуба, можно нарезать

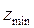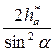==17,01 (4)

Используя выражение (3) и (4), можно определить минимальный коэффициент смещения, при котором не будет подрезания ножки зуба.

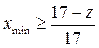
Основные способы исправления зубчатых колес (нарезание зубьев без подрезания). Из выражения (4) видно, что можно уменьшить коэффициент высоты головки зуба (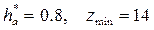) или увеличить угол профиля исходного контура a (a = 25⁰, z_min = 11). В том и другом случае инструмент будет не стандартным.

Смещение зуборезного инструмента меняет не только параметры зубчатых колес, но и зацепления в целом, поэтому при исправлении смещением, рассматривается суммарный коэффициент смещения (х_å).

Нормальное или нулевое зацепление, при котором х_å = 0, может быть в двух случаях – когда х₁ = х₂ = 0, т.е колеса не исправленные, и когда х₁ = -х₂. И в том и другом случае делительные и начальные окружности будут совпадать, т.е. a =a_w, а а =а_w (смотрите выражения (1) и (2)). При исправленных колесах это исправление будет называться высотным, так как изменяется высота головки и ножки зуба.

Положительное зацепление, при котором х_å > 0. В этом случае начальные окружности будут больше делительных и a < a_w, а а < а_w.

Отрицательное зацепление, при котором х_å < 0. В этом случае начальные окружности будут меньше делительных и a > a_w, а а > а_w.

В последних двух случаях такое исправление называется угловым.

Дата добавления: 2014-01-14