Математическая сторона задачи

Физическая сторона задачи

Запишем закон Гука для плоского напряженного состояния:

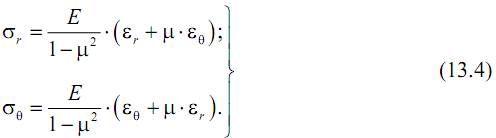
Подставив выражения (13.2) и (13.3) в формулы (13.4), получим

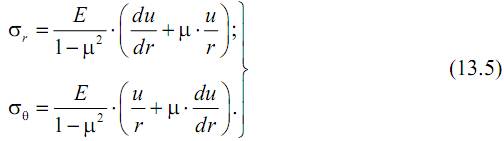
После подстановки выражений (13.5) в уравнение равновесие (13.1) получим линейное дифференциальное уравнение 2-го порядка с переменными коэффициентами относительно u:

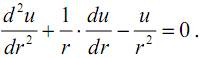
Общее решение этого уравнения выглядит следующим образом:

Подставляя решение (13.6) в формулы (13.5), получим выражения для определения напряжений в точках на расстоянии r от оси цилиндра:

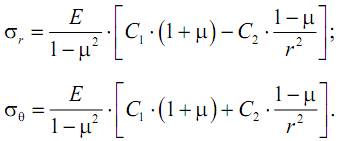
Постоянные интегрирования C1 и C2 найдем из граничных условий, а именно – на внешней поверхности цилиндра радиальные напряжения равны внешнему давлению, а на внутренней – внутреннему:

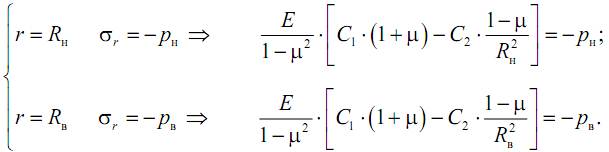
Решая полученные уравнения совместно, найдем, что

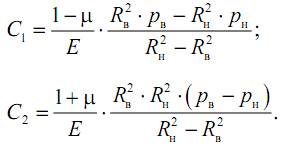
Окончательно выражения для σθ и σr запишем следующим образом:

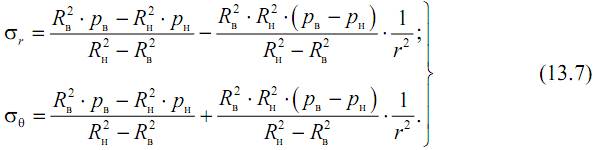
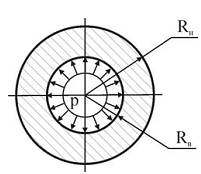Расчет толстостенных цилиндров на прочность рассмотрим для частного случая, когда имеет место только внутреннее давление (pн=0, pв=p). Здесь выражения (13.7) приобретут следующий вид:

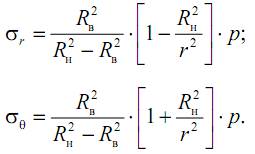
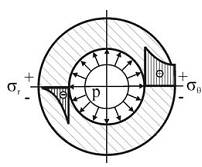Отметим, что радиальные напряжения σr в этом случае всюду сжимающие, а окружные σθ – всюду растягивающие (то есть σ1=σθ, σ3=σr) и достигают наибольших значений на внутренней поверхности цилиндра (r=Rв):

Запишем условие прочности по III теории прочности:

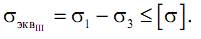
Учитывая (13.8), найдем, что

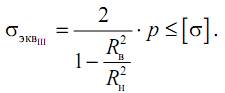
Определим допускаемое внутреннее давление в цилиндре при безграничном увеличении толщины стенки, то есть при Rн→∞. В этом случае

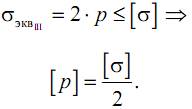
Как видим, начиная с определенного внутреннего давления [p], увеличение толщины стенки цилиндра перестает быть эффективным способом увеличения прочности. Дальнейшее увеличение прочности возможно либо за счет использования более прочных материалов (увеличение [σ]), либо за счет мероприятий, направленных на создание внешнего давления на наружной поверхности цилиндра (см. формулу (13.7)). Для этого можно, например, сделать цилиндр составным, при этом его внутренний слой необходимо запрессовать с натягом в наружный, за счет чего и создается внешнее давление на поверхности внутреннего слоя.

13.2. Расчет тонкостенных сосудов (оболочек). Уравнение Лапласа

В различных областях техники широко применяются такие элементы конструкций, которые с точки зрения их расчета на прочность могут быть отнесены к тонким оболочкам (цистерны, резервуары, баллоны и т. д.).

При расчете тонкостенных оболочек для упрощения решения задачи принимают ряд гипотез. Наиболее просто данная задача решается в рамках без моментной теории оболочек, согласно которой из шести внутренних усилий отлична от нуля лишь нормальная к сечению сила (мембранная сила), а все моменты и поперечные силы равны нулю.

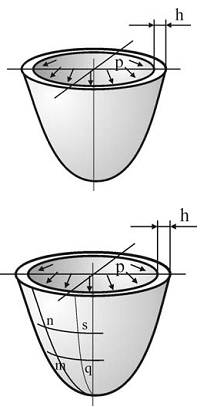Рассмотрим сосуд, имеющий форму тела вращения и подверженный внутреннему давлению p, симметрично распределенному относительно оси вращения.

Выделим элемент mnsq, вырезанный из стенки сосуда двумя меридиональными сечениями mn и sq и двумя сечениями mq и ns, нормальными к меридиану. Из-за симметрии по граням элемента mnsq будут действовать только нормальные напряжения: σm – меридиональные, σt – окружные, равнодействующая которых и будет уравновешивать внутреннее давление в сосуде.

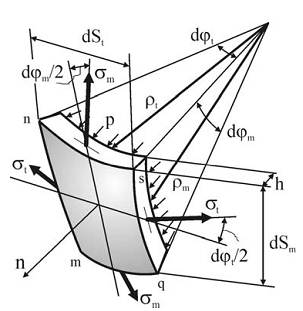
Запишем уравнение равновесия элемента mnsq, проецируя все силы на нормаль n к его поверхности:

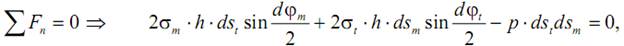
где h – толщина стенки; dst, dsm – размеры элемента в окружном и меридиональном направлениях; dϕt, dϕm – центральные углы в окружном и меридиональном направлениях, соответствующие граням элемента.

Учитывая, что ввиду малости углов

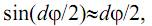
а также, что

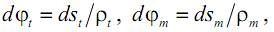
перепишем уравнение равновесия следующим образом:

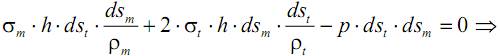
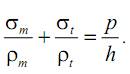
Это основное уравнение, связывающее напряжения для тонкостенных сосудов вращения, впервые дано Лапласом (уравнение Лапласа).

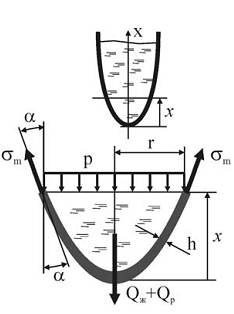Второе уравнение получим, рассмотрев равновесие нижней части резервуара с сечением радиуса r, ортогональным к оси вращения сосуда. В этом случае давление жидкости в отрезанной части сосуда p, ее собственный вес Qж и вес самого отсеченного резервуара Qр будут уравновешиваться меридиональными напряжениями на грани отсеченной части:

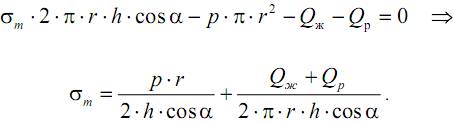
Данное выражение часто именуется уравнением равновесия зоны или просто уравнением зоны.

Зная уравнение меридиональной кривой можно найти α, r, Qж и Qр, а стало быть и σm.

Дата добавления: 2014-01-14