Лекция 14. Бесконечно малые функции и их свойства

Бесконечно малые функции и их свойства. Основные теоремы о пределах. Замечательные пределы. Натуральный логарифм и гиперболические функции.

Определение 14.1. Функция у=α(х) называется бесконечно малой при х→х₀, если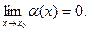

Свойства бесконечно малых.

1. Сумма двух бесконечно малых есть бесконечно малая.

Доказательство. Если α(х) и β(х) – бесконечно малые при х→х₀, то существуют δ₁ и δ₂ такие, что | α(x)|<ε/2 и |β(x)|<ε/2 для выбранного значения ε. Тогда | α(x)+β(x)|≤|α(x)|+|β(x)|<ε, то есть |(α(x)+β(x))-0|<ε. Следовательно,, то есть α(х)+β(х) – бесконечно малая.

Замечание. Отсюда следует, что сумма любого конечного числа бесконечно малых есть бесконечно малая.

1. Если α(х) – бесконечно малая при х→х₀, а f(x) – функция, ограниченная в некоторой окрестности х₀, то α(х)f(x) – бесконечно малая при х→х₀.

Доказательство. Выберем число М такое, что | f(x)|<M при | x-x₀|< δ₁, и найдем такое δ₂, что | α(x)|<ε/M при | x-x₀ |<δ₂. Тогда, если выбрать в качестве δ меньшее из чисел δ₁ и δ₂, |α (x)·f(x)|<M·ε/M=ε, то есть α(х)·f(x) – бесконечно малая.

Следствие 1. Произведение бесконечно малой на конечное число есть бесконечно малая.

Следствие 2. Произведение двух или нескольких бесконечно малых есть бесконечно малая.

Следствие 3. Линейная комбинация бесконечно малых есть бесконечно малая.

1. (Третье определение предела). Если , то необходимым и достаточным условием этого является то, что функцию f(x) можно представить в виде f(x)=A+α(x), где α(х) – бесконечно малая при х→х₀.

Доказательство.

1) Пусть Тогда | f(x)-A |<ε при х→х₀, то есть α(х)=f(x)-A – бесконечно малаяпри х→х₀. Следовательно, f(x)=A+α(x).

2) Пусть f(x)=A+α(x). Тогда 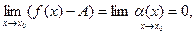значит, 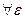| f(x)-A |<ε при | x - x₀ | < δ(ε). Cледовательно, .

Замечание. Тем самым получено еще одно определение предела, эквивалентное двум предыдущим.

Дата добавления: 2014-01-14