
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вывод уравнения концентрации
|
|
|
|
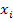 =
= 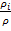 =>
=>  =
=  – концентрация (массовая или мольная). Тогда из уравнения неразрывности для многокомпонентной среды получаем:
– концентрация (массовая или мольная). Тогда из уравнения неразрывности для многокомпонентной среды получаем:
ρ[  +
+  grad
grad 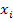 ]+
]+ 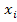 [
[ 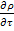 +div
+div  ]=- div
]=- div 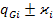 =
=  -div
-div 
 =[
=[ 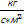 ]=
]= 
µ=f(T,P,U, 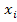 )-химический потенциал. Это работа образования одного моля i-компонента.
)-химический потенциал. Это работа образования одного моля i-компонента.
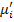 - поток химического потенциала i-компонента.
- поток химического потенциала i-компонента.
 =ρ[
=ρ[ 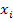 (
(  )∇
)∇ 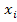 +
+ 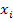 (
(  ) ∇
) ∇  +
+ 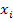 (
(  ) ∇
) ∇  +
+  ∇U+…]
∇U+…]
=ρ[ 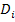 ∇
∇ 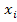 +
+  ∇T+
∇T+  ∇P+
∇P+ 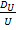 ∇U]=ρ[∇
∇U]=ρ[∇ 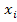 +
+  ∇T+
∇T+ 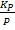 ∇P+
∇P+  ∇U], где
∇U], где 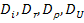 - коэффициенты диффузии, термодиффузии, бародиффузии, электродиффузии;
- коэффициенты диффузии, термодиффузии, бародиффузии, электродиффузии; 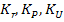 - термо, баро, электродифузиозные коэффициенты- результат нормирования соответствующих коэффициентов различных видов диффузии i компонента
- термо, баро, электродифузиозные коэффициенты- результат нормирования соответствующих коэффициентов различных видов диффузии i компонента 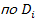
 =
= 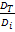 ;
;  =
= 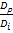 ;
; 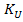 =
= 
Выражение учитывает сумму потоков массы i компонента, вызванных изменением концентраций температур, давлений, электрических потенциалов и т.д.
ρ[  +
+  grad
grad 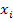 ]= -ρdiv[
]= -ρdiv[ 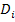 ∇
∇ 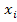 +
+  ∇T+
∇T+ 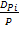 ∇P+
∇P+ 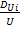 ∇U]
∇U] 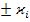 -уравнение концентрации для i компонента
-уравнение концентрации для i компонента
 +
+ 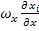 +
+ 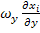 +
+ 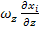 = -
= -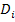 [
[  +
+ 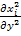 +
+ 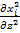 ]
]  - частный случай уравнения концентрации i компонента для изотропных условий и в пренебрежении другими видами диффузии в декартовой системе координат (уравнение Фика).
- частный случай уравнения концентрации i компонента для изотропных условий и в пренебрежении другими видами диффузии в декартовой системе координат (уравнение Фика).
В частном случае для стационарного диффузиозного (молекулярного) переноса массы имеем:
div(- 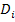 grad
grad 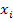 )=0
)=0
- 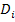 grad
grad 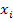 =const-закон Фика
=const-закон Фика
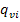 =-
=- 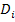 grad
grad 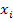 -удельный объемный поток i компонента
-удельный объемный поток i компонента
 =-
=-  grad
grad 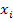 - удельный массовый поток i компонента
- удельный массовый поток i компонента
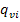 =𝛽△
=𝛽△ 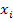 = -
= -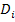 grad
grad 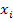 =-
=-  => 𝛽 =
=> 𝛽 =  - коэффициент массоотдачи. Получен по аналогии с коэффициентом теплоотдачи. Удельный объемный поток i-го компонента.
- коэффициент массоотдачи. Получен по аналогии с коэффициентом теплоотдачи. Удельный объемный поток i-го компонента.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 870; Нарушение авторских прав?; Мы поможем в написании вашей работы!