Построение вариационного ряда

Классификация выборок

Выборки отличаются друг от друга в зависимости от метода и способа отбора, а также степени охвата единиц совокупности. На рис. 14.1. приведена классификация выборок.

Рис. 14.1.

Определение 14.4. Повторный отбор – когда каждый элемент, случайно отобранный и обследованный, возвращается в общую совокупность и может быть повторно отобран. При этом численность единиц генеральной совокупности не изменяется в процессе отбора.

Определение 14.5. Бесповторный отбор – когда отобранный элемент не возвращается в общую совокупность. Таким образом, численность единиц генеральной совокупности сокращается в процессе отбора.

Определение 14.6. К собственно-случайной выборке относится отбор единиц из всей генеральной совокупности посредством жеребьевки или иного подобного способа, например с помощью таблицы случайных чисел.

Определение 14.7. Механический отбор применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, телефонные номера респондентов и т.д.). Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотношением выборочной и генеральной совокупностей. Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы. Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица.

Для определения предельной ошибки механической выборки используется формула предельной ошибки при собственно-случайном бесповторном отборе.

Определение 14.8. Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой её «типической» части. Типический отбор предполагает выборку единиц из каждой типической части собственно-случайным или механическим отбором.

Пусть имеется выборка объемом 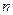. Расположим результаты выборки в таблицу:

				…
				…

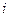
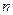
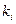
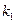
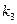
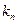
Где 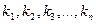– значения случайной величины 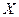соответственно в 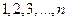испытаниях. Среди элементов выборки могут встречаться повторяющиеся. Объединив повторяющиеся значения случайной величины 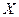, получим следующую таблицу:

				…
				…

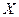
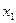
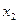
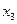
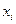
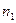
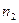
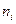
Здесь 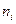– число появлений значений 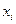. Величины называются частотами соответствующих значений 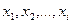случайной величины .

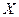Очевидно, что:

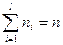(14.1)

т.е. сумма частот всех значений случайной величины 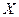равна объему выборки. Отношение частоты 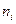к объему выборки 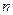называется относительной частотой значения 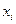и обозначается 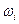. Очевидно, что:

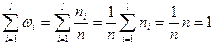(14.2)

Расположенная в порядке возрастания вариант последовательность пар чисел, составленная из вариантов и их частот 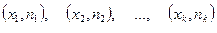называется статистическим распределением или вариационным рядом.

Пример 14.1. Рассмотрим в качестве изучаемого признака число продаж пар обуви в магазине в течение месяца для 20 продавцов: 16, 12, 15, 15, 23, 9, 15, 13, 14, 14, 21, 15, 14, 17, 8, 19, 13, 22, 17, 16.

Расположим значения признака в порядке возрастания: 8, 9, 12, 13, 13, 14, 14, 14, 15, 15, 15, 15, 16, 16, 17, 17, 19, 21, 22, 23.

Составим вариационный ряд в виде таблицы:

Число продаж,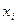

Число продавцов

Составим вариационный ряд относительных частот:

Число продаж,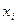
Доля продавцов	0,05	0,05	0,05	0,1	0,15	0,2	0,1	0,1	0,05	0,05	0,05	0,05

Вариация признака может быть дискретной или непрерывной.

Определение 14.4. Признак называется дискретно варьируемым, если его отдельные значения (варианты) отличаются друг от друга на некоторую конечную величину (целое число).

Определение 14.5. Признаки, значения которых отличаются друг от друга на сколько угодно малую величину, (т.е. признак может принимать любые значения в некотором интервале) называются непрерывно варьирующими.

Примеры дискретных вариационных рядов, тарифный разряд рабочего, число преступлений, и. п. К непрерывно варьирующим признакам относятся среднедушевой доход, масса человека, дальность полета снаряда и т. п.

Построение вариационного ряда на основе непрерывно варьирующего признака путем перечисления всех возможных значений признака и их частот невозможно. Выход – группировка их в некоторые интервалы с определенными границами. В интервалах запись верхней границы предыдущего интервала совпадает с нижней границей последующего. Предполагается, что каждому интервалу принадлежит лишь один из его концов, либо во всех случаях левый, либо правый. Обычно данные, полученные в результате наблюдения непрерывно варьирующего признака, представляют в виде интервального вариационного ряда. Частоты в таком ряду относятся не к отдельным значениям, а ко всему интервалу.

Пример 14.2. Менеджер большого универмага записал суммы денег, которые израсходовали 184 покупателя, посетившие отдел верхней одежды в день сезонной распродажи по сниженным ценам. Зная минимальную и максимальную стоимость покупки, менеджер сгруппировал данные о суммах, израсходованных на покупки, в следующей таблице:

Интервалы расходов	100-300	300-500	500-700	700-900	900-1100	1100-1300
Число покупателей,
Доля покупателей,	0,163	0,207	0,272	0,168	0,120	0,070

Для выбора оптимальной величины интервала (при которой вариационный ряд с равными интервалами будет не очень громоздким) применяют формулу Стэрджеса:

(14.3)

где 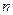– число единиц совокупности, а 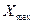и 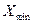– соответственно наибольшее и наименьшее значения вариантов ряда.

Определение 14.6. Разность между максимальным и минимальным элементами выборки называется размахом выборки:

(14.4)

Вариационные ряды графически могут изображаться в виде полигона или гистограммы.

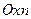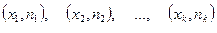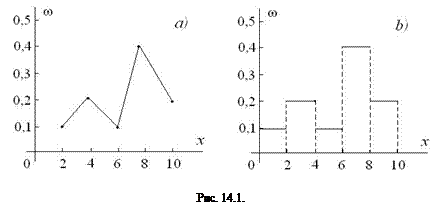
Определение 14.7. Полигоном называется ломаная линия в осях координат , вершинами которой являются точки или 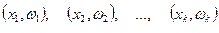, определяемые элементами статистического распределения (рис. 10.1 a).

Определение 14.8. Гистограмма – ступенчатая фигура, составленная из прямоугольников, построенных на интервалах так, что площадь каждого прямоугольника равна количеству вариант, соответствующих его основанию (рис. 14.1 b).

Гистограмма — это удобный способ представления частот сгруппированных данных в графическом виде.

Для характеристики свойств вариационного ряда наряду с понятием частоты часто используется понятие накопленной частоты.

Определение 14.9. Накопленные частоты показывают, сколько значений признака (или какая их доля) не превышает заданного значения .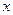

Для интервального ряда – это сумма частот всех интервалов, предшествующих данному (включая данный). Накопленные частоты можно рассчитывать в восходящем порядке (частоты вариантов суммируются сверху вниз) и нисходящем (частоты вариантов суммируются сверху вниз). В приведенной ниже таблице показаны накопленные частоты.

Таблица 14.1

Интервалы расходов,	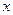100-300	300-500	500-700	700-900	900-1100	1100-1300
Число покупателей,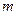
Накопленные частоты в восходящем порядке
Накопленные частоты в нисходящем порядке

Дата добавления: 2014-01-14