Сложное сопротивление. Косой изгиб

Рассмотренные нами до сих пор случаи нагружения элементов конструкций (растяжение-сжатие, сдвиг, кручение, плоский изгиб) относят сопротивление стержня к одному (простому) виду деформации. Сложным соответствует два и более простых видов.

Сложное сопротивление – вид нагружения, представляющий собой комбинацию (сочетание) нескольких простых типов сопротивления.

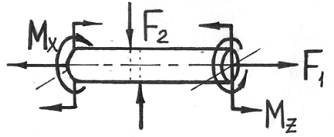
В случае сложного сопротивления в поперечных сечениях элемента возникает два и более внутренних усилия. При этом расчет элементов при сложном сопротивлении ведется в рамках принципа независимости действия сил. То есть, каждый из простых видов сопротивления, входящих в состав сложного, рассматривается независимо от остальных, а затем находится суперпозиция (сумма) полученных решений (для внутренних усилий, напряжений, деформаций и т. д.). Принцип суперпозиции применим только для линейно-упругих систем.

14.1. Общие понятия о косом изгибе

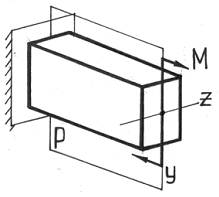Прежде чем перейти к рассмотрению некоторых характерных для инженерной практики случаев сложного сопротивления и, в частности, косого изгиба, вспомним, что до этого мы анализировали частный случай изгиба, который называли плоским, – когда плоскость действия сил совпадала с одной из главных плоскостей инерции балки. Однако существуют и более общие случаи изгиба, когда силы действуют в плоскости, не совпадающей с плоскостью инерции (косой изгиб), или, вообще, силы не лежат в одной плоскости (сложный или неплоский изгиб).

Косой изгиб – изгиб, при котором плоскость P действия изгибающих моментов и поперечных сил не совпадает ни с одной из главных плоскостей инерции бруса.

14.2. Определение внутренних усилий при косом изгибе

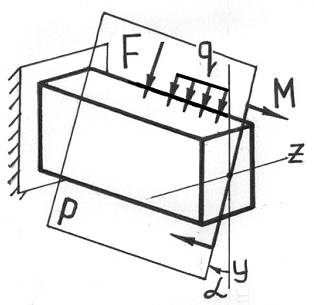
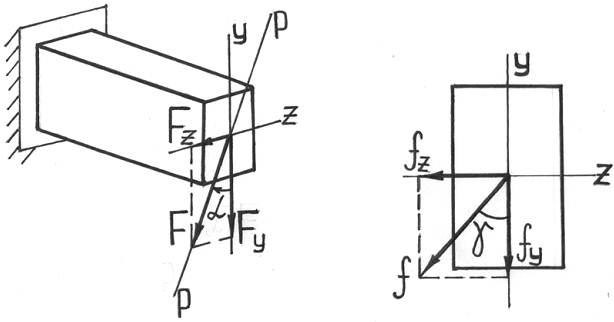
При косом изгибе в поперечных сечениях бруса действуют следующие внутренние усилия: Mz, My – изгибающие моменты и Qy, Qz – поперечные (перерезывающие) силы. Это легко показать, используя метод мысленных сечений и определяя внутренние усилия при косом изгибе консольной балки под действием сосредоточенной силы F на свободном конце (см. рисунок):

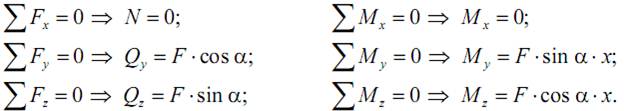
Аналогичные усилия возникают и в более общем случае сложного (неплоского) изгиба.

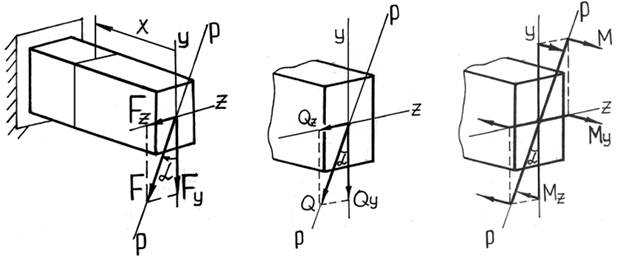
Правило знаков для внутренних усилий: изгибающие моменты – положительны, если вызывают растяжение в положительном квадранте координатной системы zOy; поперечные силы – положительны, если под их действием отсеченный элемент поворачивается по часовой стрелке.

Таким образом, косой изгиб может быть представлен как совместное действие двух плоских изгибов в двух взаимно перпендикулярных плоскостях инерции.

Для определения полного изгибающего момента M и полной поперечной силы Q при косом изгибе достаточно определить внутренние усилия для каждого из плоских изгибов в отдельности (то есть Qy, Mz и Qz, My), а затем найти их векторную сумму:

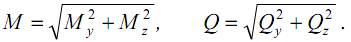
4 .3. Определение напряжений при косом изгибе

Используя принцип независимости действия сил (принцип суперпозиции) найдем напряжения при косом изгибе. Рассмотрим точку A с координатами (y, z) в сечении изгибаемой балки и определим в ней напряжения от каждого из внутренних усилий, возникающих при косом изгибе:

нормальные напряжения от изгибающего момента Mz

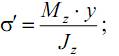
нормальные напряжения от изгибающего момента My

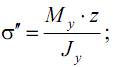
касательные напряжения от поперечной силы Qy

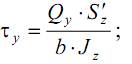
касательные напряжения от поперечной силы Qz

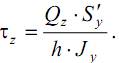
Полные напряжения τ и σ при косом изгибе найдем путем геометрического суммирования составляющих:

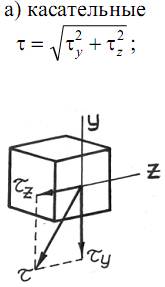
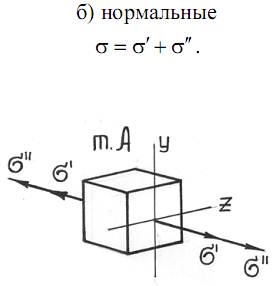
Последнюю формулу удобно представить в виде

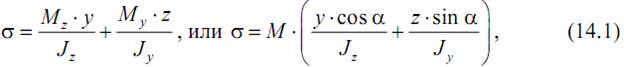
где α – угол наклона силовой плоскости P при косом изгибе (а при сложном изгибе α – угол наклона плоскости действия полного изгибающего момента M в данном сечении).

14.4. Определение положения нейтральной оси и максимальных нормальных напряжений при косом изгибе. Условие прочности

Нейтральная ось – линия, во всех точках которой нормальные напряжения равны нулю. При этом в точках сечения, наиболее удаленных от нейтральной оси нормальные напряжения принимают свои экстремальные значения – минимум и максимум.

Заметим, что при плоском изгибе нейтральная ось совпадала с одной из главных осей сечения (Oy или Oz), при косом же изгибе это не так. Выведем формулу для определения положения нейтральной оси при косом изгибе.

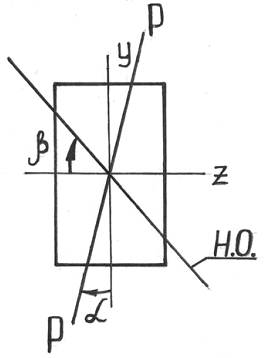
Так как σ=0, то можем записать

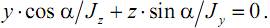
Отсюда найдем уравнение нейтральной оси:

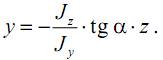
Более удобно записать это уравнение через угол β наклона нейтральной линии к оси Oz:

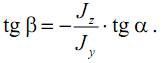
Знак «минус» в этой формуле показывает, что углы α и β откладываются от разноименных осей, но в одном направлении.

Как видим, в случае, когда Jz≠Jy, углы α и β не равны друг другу, а, значит, и плоскость кривизны (плоскость максимальных прогибов) бруса не будет совпадать с плоскостью действия сил. Поэтому такой изгиб и назван «косым».

Определим максимальные нормальные напряжения при косом изгибе и запишем условие прочности.

Как известно, нормальные напряжения достигают своих экстремальных значений σextr в точках, наиболее удаленных от нейтральной оси (координаты таких точек обозначим yуд. и zуд.). Стало быть, можем записать:

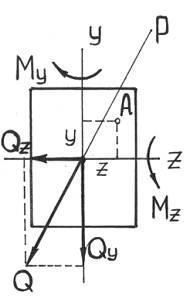
Для прямоугольного сечения – это точки A и B. При M>0

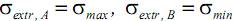(см. рисунок).

Для материалов, одинаково сопротивляющихся растяжению (сжатию), максимальные напряжения определяются так:

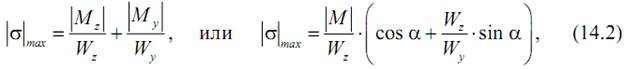
Где 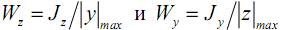– моменты сопротивления сечения относительно осей z и y.

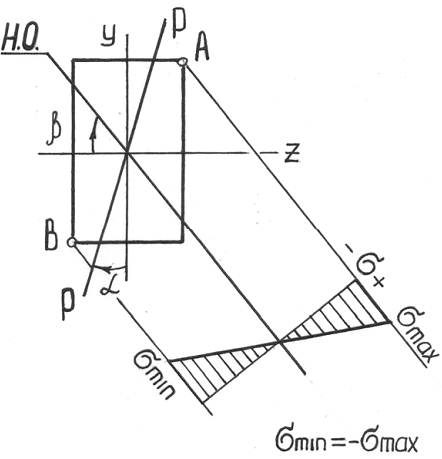
В случае косого изгиба, как правило, проверка прочности осуществляется лишь по нормальным напряжениям (действие касательных невелико). Поэтому условие прочности запишем в виде:

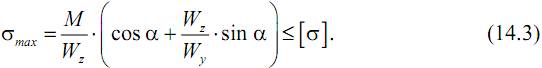
При косом изгибе (впрочем, как и при остальных видах нагружения) имеем три задачи расчета на прочность: 1) проверка прочности [проверить неравенство (14.3) – «выдержит - не выдержит»]; 2) подбор сечения [определить Wz (размеры сечения), при заданном отношении Wz/Wy]; 3) проверка по несущей способности (определить M).

14.5. Деформации при косом изгибе

Рассматривая косой изгиб как совокупность двух плоских, полную деформацию балки можем найти, геометрически суммируя деформации балки от плоских изгибов во взаимно перпендикулярных плоскостях:

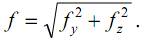
Проанализируем косой изгиб консольной балки прямоугольного сечения. Разложим силу F, изгибающую балку, на две составляющие Fy=F·cosα и Fz=F·sinα и найдем деформации от каждой из них:

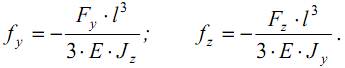
Суммарная деформация

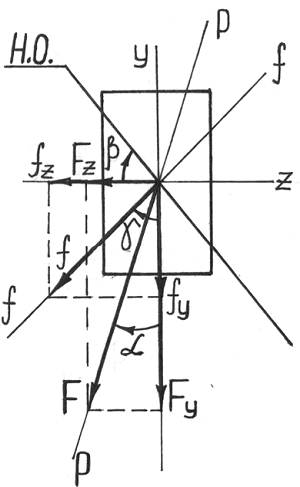
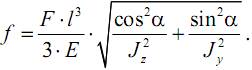
Определим положение плоскости, в которой происходит изгиб балки, для чего найдем величину угла γ между этой плоскостью и осью Oy:

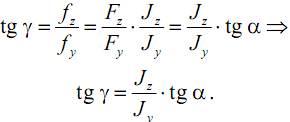
Как видим, плоскость прогибов не совпадает с силовой плоскостью (α≠γ – «косой» изгиб!) и перпендикулярна нейтральной оси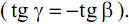

Дата добавления: 2014-01-14