
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
АсимптотичеCкие методы решения краевых задач
|
|
|
|
Отслеживание состояния DataSet
В предыдущей части Вы узнали, как использовать TDataSource, чтобы узнать текущее состоянии TDataSet. Использование DataSource - это простой путь выполнения данной задачи. Однако, если Вы хотите отслеживать эти события без использования DataSource, то можете написать свои обработчики событий TTable и TQuery:
property OnOpen
property OnClose
property BeforeInsert
property AfterInsert
property BeforeEdit
property AfterEdit
property BeforePost
property AfterPost
property OnCancel
property OnDelete
property OnNewRecord
Большинство этих свойств очевидны. Событие BeforePost функционально подобно событию TDataSource.OnUpdateData, которое объяснено выше. Другими словами, программа STATE работала бы точно также, если бы Вы отвечали не на DataSource1.OnUpdateData а на Table1.BeforePost. Конечно, в первом случае Вы должен иметь TDataSource на форме, в то время, как во втором этого не требуется.
(методы возмущений)
Многие задачи, с которыми сталкиваются физики, инженеры и специалисты по прикладной математике, не поддаются точному решению. Среди причин, затрудняющих точное решение, можно указать, например, нелинейность уравнений, переменность коэффициентов, нелинейность граничных условий на известных или неизвестных границах сложной формы и др. Для решения подобных задач мы вынуждены пользоваться различного рода приближениями, комбинируя аналитические и численные методы.
Среди аналитических методов весьма мощными являются методы возмущений (аналитических разложений) по большим или малым значениям параметра или координаты.
Любые исследования имеют дело с моделями реальных процессов, объектов. Модели (уравнения) дают лишь приближенные описания явлений, объекта исследования. В процессе создания модели стараемся принять во внимание одни особенности задачи, полностью пренебрегаем другими и лишь в определенной степени учитываем третьи. Для осуществления этих важных шагов, прежде всего, необходимо определить порядок величин различных элементов системы, сравнивая их друг с другом или (и) с заранее выбранными характерными величинами. Прежде чем пытаться проделать какие-либо аппроксимации (упрощения), всегда нужно ввести безразмерные переменные. Далее исследователь всегда «упрощает» задачу, отбрасывая слагаемые и понижая порядок системы (уравнений, модели). Возможность такого упрощения обычно оправдывается малостью того или иного параметра. Однако не всякую малую величину можно отбросить, не искажая смысл задачи. Поэтому необходимо иметь методы, позволяющие изучать зависимость решений от параметров задачи и, прежде всего, асимптотическое поведение решений при их малых значениях.
Асимптотические решения представляются в виде одного или нескольких рядов, каждый член которых удовлетворяет более простому, чем исходное, уравнению. Возникающие при решении неизвестные постоянные и структура асимптотического разложения определяются с помощью процедуры сращивания. Важно подчеркнуть, что наличие малого или большого параметра во многих случаях обусловлено постановкой задачи, а не желанием исследователя получить тот или иной аналитический результат. Строгое математическое обоснование асимптотических методов в настоящее время находится еще в сравнительно зачаточном состоянии. Получающиеся при использовании методов возмущений асимптотические ряды часто расходятся или крайне медленно сходятся.
Методы возмущений представляют собой одно из проблем наиболее мощных средств современной ПМ и служат для выяснения принципиально важных закономерностей и качественных особенностей весьма сложных линейных и нелинейных краевых задач, для получения асимптотик и анализа решений в окрестности особых точек, для построения «тестовых» решений, а в ряде случаев являются также основой для разработки вычислительных методов.
1. Примеры. Рассмотрим движение частицы массы  , закрепленной на линейной пружине с коэффициентом жесткости
, закрепленной на линейной пружине с коэффициентом жесткости  и испытывающий сопротивление среды, коэффициент вязкости которой равен
и испытывающий сопротивление среды, коэффициент вязкости которой равен 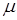
































 k
k  Тогда по второму закону Ньютона имеем
Тогда по второму закону Ньютона имеем

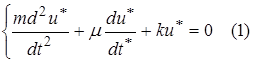

 - смешение частиц,
- смешение частиц,
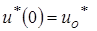 ,
,  . Введем безразмерные переменные
. Введем безразмерные переменные 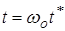 ,
,
 (
(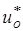 - некоторый характеристический масштаб длины)
- некоторый характеристический масштаб длины) 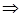
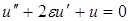 (2), где
(2), где  , представляет соотношение силы сопротивления к силе инерции (упругой возвращающей силе пружины),
, представляет соотношение силы сопротивления к силе инерции (упругой возвращающей силе пружины),
 - угловая частота колебания.
- угловая частота колебания.
Рассмотрим решение уравнения (2) при малых 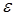 и прямое разложение
и прямое разложение
 (3)
(3)
из(2) 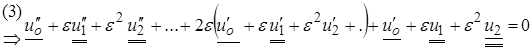 (4)
(4)
Группируя члены с одинаковыми степенями 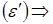
 (5)
(5)
Приравнивая нулю коэффициенты при соответствующих степенях 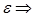
 (6) Þ
(6) Þ  , (7)
, (7)
где 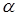 и
и - постоянные интегрирования.
- постоянные интегрирования.
(6.2) Þ  (8) Þ частные решения
(8) Þ частные решения 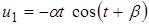 (9)
(9)
(6.3) Þ 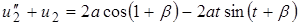 Þ (10)
Þ (10)
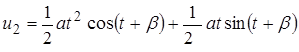 (11)
(11)
Тогда (3) Þ  (12)
(12)
Полученное прямое или линейное разложение оказывается непригодным при 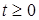
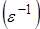 из-за наличия в нем сакулярных членов.
из-за наличия в нем сакулярных членов.
Точное решение уравнения (2): Допускается решение вида
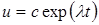 (13)
(13) 
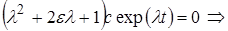
действительные решения:  (14)
(14)
Для того, чтобы выяснить причину неравномерности прямого разложения, разложим (14) при малых 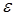 , найдем первые три члена этого разложения и сравним полученный результат с прямым разложением (12)
, найдем первые три члена этого разложения и сравним полученный результат с прямым разложением (12)
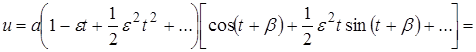
 (15)
(15)
Хотя (15) находится в полном соответствии с разложением (12), отметим несостоятельность прямого разложения (14) при больших  обусловленного разложением функций
обусловленного разложением функций 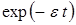 и
и 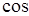
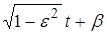 в ряды по степеням
в ряды по степеням 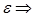 . Любая процедура разложения, не учитывающая зависимость частоты колебаний системы от величины параметра
. Любая процедура разложения, не учитывающая зависимость частоты колебаний системы от величины параметра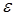 , окажется несостоятельной при больших
, окажется несостоятельной при больших 

 ,
, 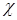 - коэффициент температуропроводности.
- коэффициент температуропроводности.
П. Задачи с пограничным слоем
Рассмотрим задачи с возмущениями, действующими в очень узких областях или зонах, в которых зависимые переменные испытывают достаточно резкие изменения. Ввиду наличия малого параметра при старшей производной эти узкие зоны часто оказываются лежащими вблизи границы области, в которой решается задача. Поэтому в задачах механики жидкостей и газов такие зоны называют обычно пограничными слоями, в механике твердого тела – областями краевого эффекта, в электрических приложениях – поверхностными (или скин-слоями). Во многих физических задачах резкие изменения зависимых переменных часто происходят внутри интересующих нас областей. В таких случаях узкие зоны, где эти изменения имеют место, в МЖГ и механике твердого тела называют обычно ударными слоями (скачками уплотнения), в квантовой механике - точками перехода и т.д. Указанные быстрые изменения мы можем исследовать с помощью обычных медленных масштабов Þ. Это приводит к необходимости вводить новые – быстрые, увеличенные или растянутые переменные.
Существует большое число методов исследования задач с пограничным слоем, как, например, метод сращиваемых асимптотических разложений, метод составных разложений, метод многих масштабов, метод ВКБ и преобразование Лангера.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 610; Нарушение авторских прав?; Мы поможем в написании вашей работы!