Метод сращиваемых асимптотических разложений

Рассмотрим краевую задачу

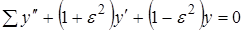(2.1)

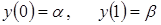(2.2)

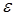- малый безразмерный параметр. Решение ищем в виде:

(2.3)

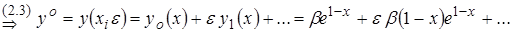(2.1) (2.4)

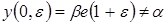. Поэтому рассмотрим точное решение (2.1) – линейное дифференциальное уравнение с постоянными коэффициентами Þ

(2.5)

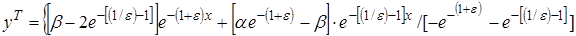
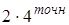
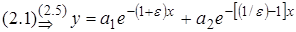(2.6) После определения постоянных интегрирования и разложения в ряд при малых 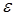Þ 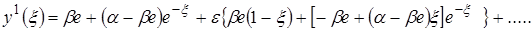(2.4²)

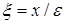
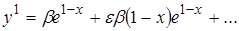, (2.4¢)

которое находится в полном соответствии с разложением (2.4).

Решение (2.4¢) также является непригодным при (вблизи) х=0, т.к. видимо, воспользовавшись необоснованными операциями при разложении (2.4², записанного в терминах 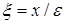) и 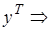(2.4) и (2.4 точн.) согласуются везде, за исключением малого участия вблизи точки х=0, где

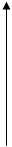
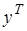быстро меняется, чтобы успеть удовлетворить граничному условию 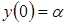. Этот участок вблизи начала координат называют пограничным слоем. y

4,0 Имеется неравномерная сходимость прямого

разложения (2.4) 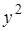к точному решению зада-

2,0 чи 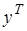Þ. Нельзя ли построить равно-

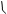
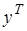
мерно пригодное разложение, исполь-

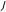зуя в качестве масштаба не пере-

0,25 0,5 0,75 1,0 x

менную 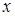, а некоторую функцию 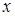и .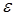

Введем 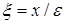.Используя точное решение (2.4^точн) и его разложение при малых 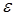и фиксированном 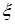получим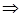

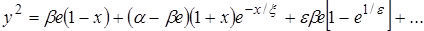(2.7)

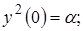
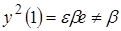. Данное решение согласуется с точным решением в малой окрестности 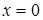, но сильно отклоняется от него вдали от этой точки.

Для решения подобных задач используют метод сращиваемых асимптотических разложений (кроме метода многих масштабов).

Основная идея метода состоит в том, что приближенное решение задачи ищется не в виде единого разложения с заданным масштабом переменных, а в виде нескольких отдельных разложений, в которых используются два или более различных масштаба, пригодные лишь в части рассматриваемой области. Эти масштабы выбираются таким образом, чтобы 1) полный набор разложений охватывал всю интересующую нас область и 2) области применимости соседних разложений перекрывались. При этом ввиду условия 2) нам необходимо срастить (т.е. согласовать друг с другом) соседние разложения и, тем самым, связать их между собой.

Основную идею сращивания можно рассмотреть на примере сращивания разложения 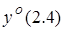с 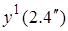, которые были найдены путем разложения 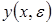соответственно при фиксированном 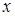и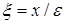

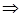
Какое влияние на эти два разложения оказывает переход от одного масштаба переменной к другому?

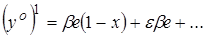(2.8.1)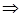

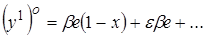(2.8.2)

Внешнее разложение внутреннего разложения равно внутреннему разложению внешнего разложения (2.9)

Правило (2.9) применимо только в том случае, когда два соседних разложения имеют перекрывающиеся области применимости. Это правило называется принципом сращивания и служит для сращивания двух соседних разложений.

Ш. ВКБ метод (Вентцеля, Крамера, Бриллюэна)

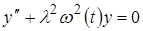(3.1)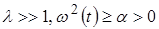

Решение ищется в виде 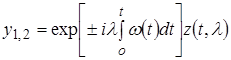(3.2)

Функция 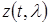меняется медленно

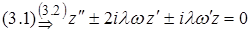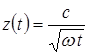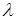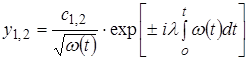(3.3) Þ при больших Þ (3.4)

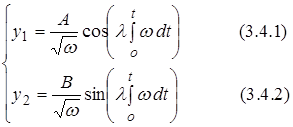
При 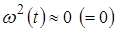(3.1) точки поворота (перехода).

Дата добавления: 2014-01-14