Сложное сопротивление. Кручение с изгибом

16.1. Общие понятия и определения

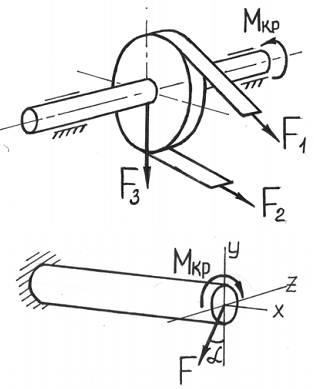Ранее нами был рассмотрен расчет на прочность валов при чистом кручении. Однако круглые валы редко работают на чистое кручение. Как правило, при работе вал изгибается собственным весом, весом шкивов, давлением на зубья шестерен, натяжением ремней и т. д. В таком случае вал будет находиться в условиях сложного сопротивления и испытывать совместное действие кручения и изгиба.

Кручение с изгибом – частный случай сложного сопротивления, который может рассматриваться как сочетание чистого кручения и поперечного изгиба.

16.2. Определение внутренних усилий и напряжений при кручении с изгибом

Для определения внутренних усилий воспользуемся методом мысленных сечений:

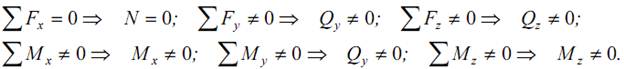
Обычно две составляющие поперечной силы (Qy, Qz) и изгибающего момента (My, Mz) приводят к их полным результирующим

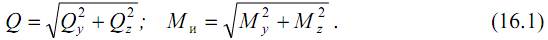
Заметим, что часто поперечной силой пренебрегают (для достаточно длинных валов) и рассматривают кручение с изгибом как совместное действие крутящего (Mx, Mкр, T) и изгибающего (Mи) моментов.

Опасное сечение вала будем искать, как и прежде, по эпюрам внутренних усилий. При построении эпюр внутренних усилий при кручении с изгибом необходимо иметь ввиду следующие правила:

1) эпюры крутящего момента Mx, а также эпюры составляющих поперечной силы Qy, Qz и изгибающего момента My, Mz строятся по той же процедуре, что и ранее;

2) результирующая поперечная сила Q может не лежать в плоскости действия результирующего изгибающего момента Mи, а потому между ними уже не будет соблюдаться зависимость Журавского (dM/dx=Q), а, следовательно, и правила проверки эпюр, введенные для плоского изгиба;

3) согласно (16.1), эпюра полного изгибающего момента будет прямой только на тех участках, где My и Mz ограничены прямыми с общей нулевой точкой, на участках, где такая общая точка отсутствует эпюра Mи будет описываться вогнутой кривой и строится по точкам (связано с тем, что вектор Mи в разных сечениях имеет различное направление).

Опасное сечение при кручении с изгибом устанавливается из совместного анализа эпюр крутящего Mx и полного изгибающего Mи моментов. Опасным будет считаться то сечение, где оба момента достигают своей максимальной величины. Если моменты достигают максимума в разных сечениях, необходимо проверить все сечения, в которых эти внутренние усилия достаточно велики.

Для определения максимальных напряжений ис-пользуем принцип независимости действия сил и найдем напряжения отдельно от кручения и отдельно от изгиба:

а) напряжения при кручении

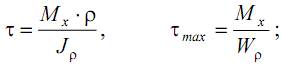
б) напряжения при изгибе

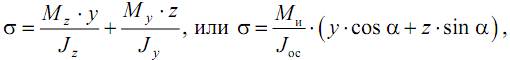
где Jос – осевой момент инерции для круглого сечения (Jос=Jz=Jy). Вводя обозначение 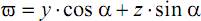, можем записать

Wос – осевой момент сопротивления для круглого сечения(Wос=Jос/ρmax, ρmax=d/2).

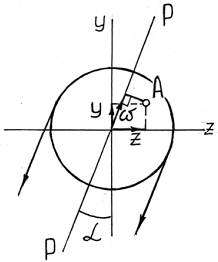
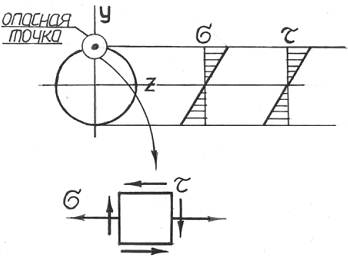Опасными точками в сечении будут являться точки наиболее удаленные от нейтральной оси (для круглого сечения – линии, перпендикулярной плоскости действия результирующего изгибающего момента). При этом в токах сечения будет возникать плоское напряженное состояние, а потому расчет на прочность необходимо проводить с привлечением известных теорий прочности.

16.3. Определение главных напряжений и расчет на прочность при кручении с изгибом

Подставив величины максимальных нормальных и касательных напряжений в формулу для главных напряжений (σ2=0), получим:

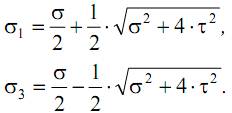
Расчет брусьев при изгибе с кручением проводится с применением теорий прочности. При этом расчет элементов из пластичных материалов выполняется на основе III или IV теорий прочности, а из хрупких – по теории Мора. Проанализируем расчет на прочность по III теории прочности

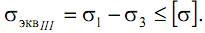
Подставляя в эту формулу выражения для главных напряжений, получим:

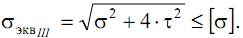
Запишем условие прочности через крутящий и изгибающий моменты, учитывая, что для круглого сечения Wp=2·Wос:

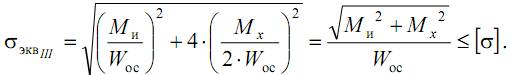
Выражение под корнем называют приведенным (эквивалентным) моментом по третьей теории:

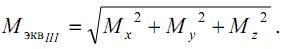
Окончательно условие прочности запишем в виде

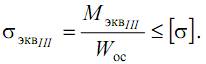
Проанализируем расчет на прочность по IV теории прочности

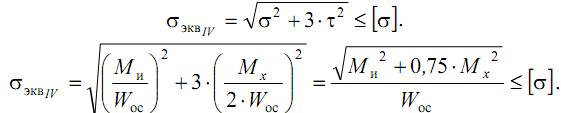
Приведенный (эквивалентный) момент по четвертой теории:

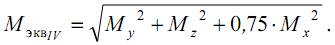
Окончательно условие прочности запишем в виде

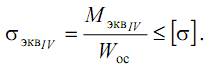
Дата добавления: 2014-01-14