Оптимизация нечеткого регулятора

Рассмотрим использование генетических алгоритмов для оптимизации нечеткого регулятора. Генетические алгоритмы – адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основаны на подобии генетическим процессам биологических организмов: биологические популяции развиваются в течении нескольких поколений, подчиняясь законам естественного отбора и по принципу "выживает наиболее приспособленный" (survival of the fittest), открытому Чарльзом Дарвином. Подражая этому процессу генетические алгоритмы способны "развивать" решения реальных задач, если те соответствующим образом закодированы.

Генетические алгоритмы работают с совокупностью "особей" - популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее "приспособленности" согласно тому, насколько "хорошо" соответствующее ей решение задачи. Наиболее приспособленные особи получают возможность "воспроизводить" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции.

Так и воспроизводится вся новая популяция допустимых решений, выбирая лучших представителей предыдущего поколения, скрещивая их и получая множество новых особей. Это новое поколение содержит более высокое соотношение характеристик, которыми обладают хорошие члены предыдущего поколения. Таким образом, из поколения в поколение, хорошие характеристики распространяются по всей популяции. В конечном итоге, популяция будет сходиться к оптимальному решению задачи.

Имеются много способов реализации идеи биологической эволюции в рамках генетических алгоритмов. Традиционный, можно представить в виде следующей блок-схемы показанной на рисунке 22, где:

1. Инициализация начальной популяции – генерация заданного числа решений задачи, с которых начинается процесс оптимизации;

2. Применение операторов кроссовера и мутации;

3. 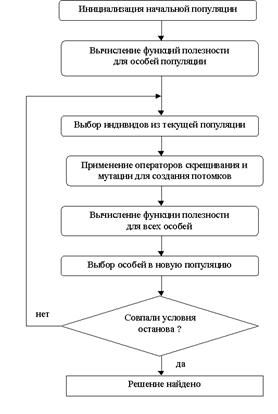Условия останова – обычно процесс оптимизации продолжают до тех пор, пока не будет найдено решение задачи с заданной точностью, или пока не будет выявлено, что процесс сошелся (т.е. не произошло улучшения решения задачи за последние N поколений).

В среде Matlab генетические алгоритмы представлены отдельным тулбоксом, а также пакетом ANFIS. ANFIS - это аббревиатура Adaptive-Network-Based Fuzzy Inference System - адаптивная сеть нечеткого вывода. ANFIS является одним из первых вариантов гибридных нейро-нечетких сетей - нейронной сети прямого распространения сигнала особого типа. Архитектура нейро-нечеткой сети изоморфна нечеткой базе знаний. В нейро-нечетких сетях используются дифференцируемые реализации треугольных норм (умножение и вероятностное ИЛИ), а также гладкие функции принадлежности. Это позволяет применять для настройки нейро-нечетких сетей быстрые и генетические алгоритмы обучения нейронных сетей, основанные на методе обратного распространения ошибки. Ниже описываются архитектура и правила функционирования каждого слоя ANFIS-сети.

ANFIS реализует систему нечеткого вывода Сугено в виде пятислойной нейронной сети прямого распространения сигнала. Назначение слоев следующее: первый слой - термы входных переменных; второй слой - антецеденты (посылки) нечетких правил; третий слой - нормализация степеней выполнения правил; четвертый слой - заключения правил; пятый слой - агрегирование результата, полученного по различным правилам.

Входы сети в отдельный слой не выделяются. На рис.23 изображена ANFIS-сеть с одной входной переменной («ошибка») и пятью нечеткими правилами. Для лингвистической оценки входной переменной «ошибка» используется 5 термов.

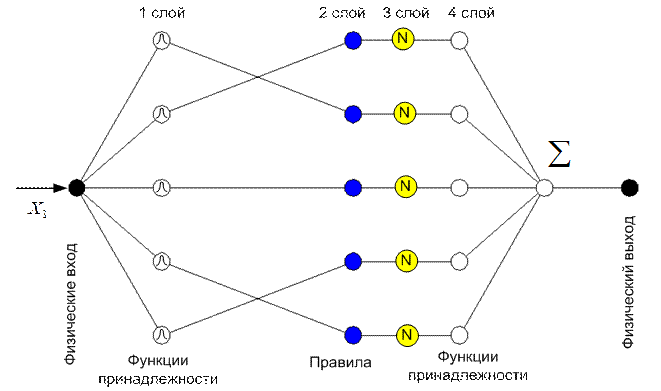
Рис.23. Структура ANFIS-сети.

Введем следующие обозначения, необходимые для дальнейшего изложения:

Пусть 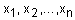- входы сети;

y - выход сети;

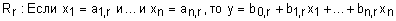- нечеткое правило с порядковым номером r;

m - количество правил,;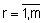

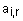- нечеткий терм с функцией принадлежности 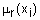, применяемый для лингвистической оценки переменной 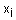в r-ом правиле (,);

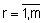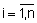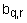- действительные числа в заключении r-го правила (,).

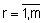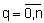ANFIS-сеть функционирует следующим образом.

Слой 1. Каждый узел первого слоя представляет один терм с колокообразной функцией принадлежности. Входы сети 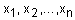соединены только со своими термами. Количество узлов первого слоя равно сумме мощностей терм-множеств входных переменных. Выходом узла являются степень принадлежности значения входной переменной соответствующему нечеткому терму:

,

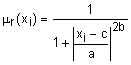где a, b и c - настраиваемые параметры функции принадлежности.

Слой 2. Количество узлов второго слоя равно m. Каждый узел этого слоя соответствует одному нечеткому правилу. Узел второго слоя соединен с теми узлами первого слоя, которые формируют антецеденты соответствующего правила. Следовательно, каждый узел второго слоя может принимать от 1 до n входных сигналов. Выходом узла является степень выполнения правила, которая рассчитывается как произведение входных сигналов. Обозначим выходы узлов этого слоя через , .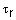

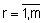Слой 3. Количество узлов третьего слоя также равно m. Каждый узел этого слоя рассчитывает относительную степень выполнения нечеткого правила:

.

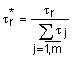Слой 4. Количество узлов четвертого слоя также равно m. Каждый узел соединен с одним узлом третьего слоя а также со всеми входами сети (на рис. 18 связи с входами не показаны). Узел четвертого слоя рассчитывает вклад одного нечеткого правила в выход сети:

.

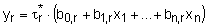Слой 5. Единственный узел этого слоя суммирует вклады всех правил:

.

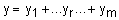Типовые процедуры обучения нейронных сетей могут быть применены для настройки ANFIS-сети так как, в ней использует только дифференцируемые функции. Обычно применяется комбинация градиентного спуска в виде алгоритма обратного распространения ошибки и метода наименьших квадратов. Алгоритм обратного распространения ошибки настраивает параметры антецедентов правил, т.е. функций принадлежности. Методом наименьших квадратов оцениваются коэффициенты заключений правил, так как они линейно связаны с выходом сети. Каждая итерация процедуры настройки выполняется в два этапа. На первом этапе на входы подается обучающая выборка, и по невязке между желаемым и действительным поведением сети итерационным методом наименьших квадратов находятся оптимальные параметры узлов четвертого слоя. На втором этапе остаточная невязка передается с выхода сети на входы, и методом обратного распространения ошибки модифицируются параметры узлов первого слоя. При этом найденные на первом этапе коэффициенты заключений правил не изменяются. Итерационная процедура настройки продолжается пока невязка превышает заранее установленное значение. Для настройки функций принадлежностей кроме метода обратного распространения ошибки могут использоваться и другие алгоритмы оптимизации, например, метод Левенберга-Марквардта.

Рис.24. Рабочая область ANFISedit.

Попробуем теперь оптимизировать нечеткий регулятор для единичного ступенчатого воздействия. Желаемый переходный процесс имеет приблизительно следующий вид:

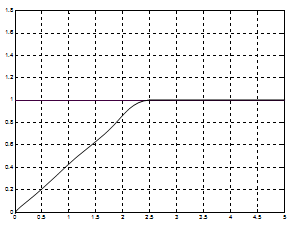
Рис.25. Желаемый переходный процесс.

Из графика изображенного на рис. следует, что большую часть времени двигатель должен работать на полную мощность, чтобы обеспечить максимальное быстродействие, а при приближении к желаемому значению должен плавно притормаживать. Руководствуясь этими простыми рассуждениями, в качестве обучающей возьмем следующую выборку значений, представленную ниже в виде таблицы:

Таблица 4

Значение ошибки	Значение управления
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
Значение ошибки	Значение управления
0.05
0.03
0.01
0.005
0.001	0.5
-0.001	-0.5
-0.005	-1
-0.01	-3
-0.03	-5
-0.05	-8
Значение ошибки	Значение управления
-0.1	-10
-0.2	-15
-0.3	-18
-0.4	-20
-0.5	-21
-0.6	-23
-0.7	-25
-0.8	-27
-0.9	-27
-1	-27
-2	-27

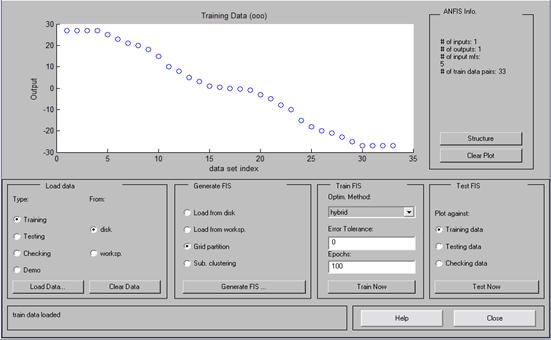
Рис.26. Вид обучающей выборки.

Обучение будем проводить на 100 шагах. Этого более чем достаточно для сходимости используемого метода.

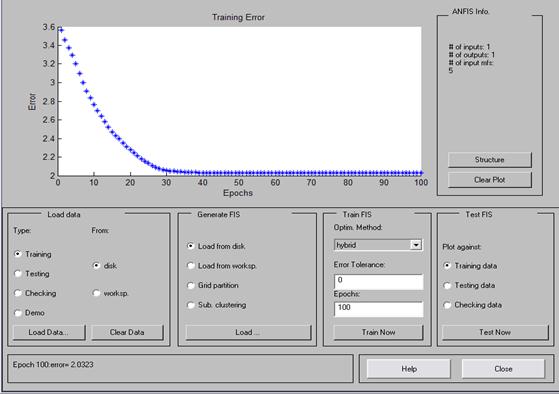
Рис.27. Процесс обучения нейросети.

В процессе обучения параметры функций принадлежности формируются таким образом, чтобы при заданной величине ошибки регулятор создавал необходимое управление. На участке между узловыми точками зависимость управления от ошибки является интерполяцией данных таблицы. Метод интерполяции зависит от способа обучения нейросети. Фактически после обучения модель нечеткого регулятора можно представить нелинейной функцией одной переменной, график которой представлен ниже.

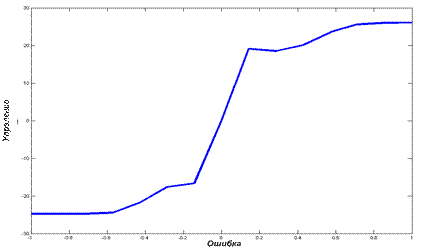
Рис.28. График зависимости управления от ошибки поп положению внутри регулятора.

Сохранив найденные параметры функций принадлежности, промоделируем систему с оптимизированным нечетким регулятором.

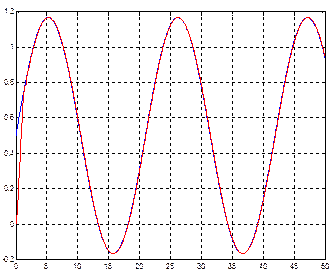
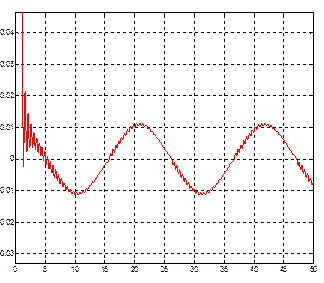
Рис. 29. Переходный процесс при гармоническом входном воздействии для модели с оптимизированным нечетким регулятором, содержащим одну входную лингвистическую переменную.

Рис.30. Сигнал ошибки при гармоническом входном воздействии для модели с нечетким регулятором, содержащим две входные лингвистические переменные.

Из графиков следует, что оптимизация нечеткого регулятора с помощью обучения нейросети удалась. Значительно снизилась колебательность и величина ошибки. Поэтому использование нейросети является вполне обоснованным для оптимизации регуляторов, принцип действия которых основан на нечеткой логике. Тем не менее, даже оптимизированный регулятор не может удовлетворить предъявленные требования по точности, поэтому целесообразно рассмотреть еще один способ управления, когда нечеткий регулятор управляет не непосредственно объектом, а занимается соединением нескольких законов управления в зависимости от сложившейся ситуации.

Дата добавления: 2014-01-14