Дефаззификатор

Таким образом, результирующее воздействие U будет определяться соответственно выполнению какого-либо правила. Если возникает ситуация, когда выполняются сразу несколько правил, то результирующее воздействие U находится по следующей зависимости:

, где n-число сработавших правил (дефаззификация методом центра области), u_n – физическое значение управляющего сигнала, сответствующее каждому из нечетких множеств UBO, UMo, UZ, UMp, UBP. mUn(u) – степень принадлежности управляющего сигнала u к соответствующему нечеткому множеству Un={ UBO, UMo, UZ, UMp, UBP }. Существуют также и другие методы дефаззификации, когда выходная лингвистическая переменная пропорциональна самомому «сильному» или «слабому» правилу.

Промоделируем процесс управления электроприводом с помощью вышеописанного нечеткого регулятора.

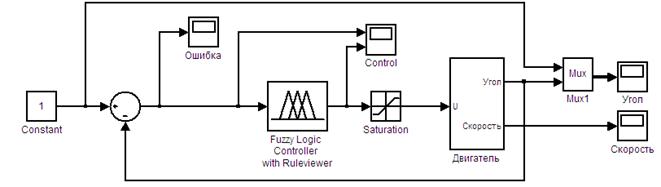Рис.10. Структурная схема системы в среде Matlab.

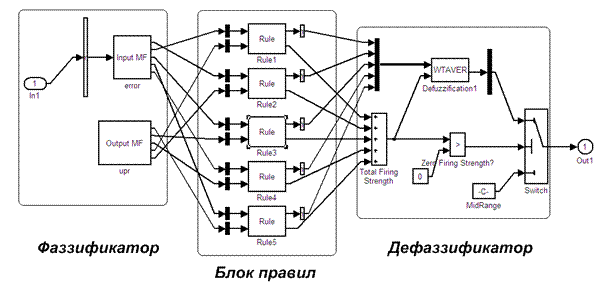
Рис.11. Структурная схема нечеткого регулятора в среде Matlab.

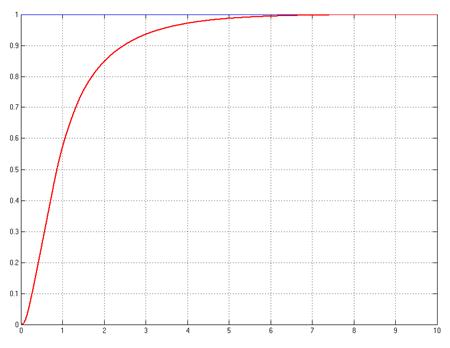
Рис.12. Переходный процесс при единичном ступенчатом воздействии.

Рис. 13. Переходный процесс при гармоническом входном воздействии для модели с нечетким регулятором, содержащим одну входную лингвистическую переменную.

Анализ характеристик привода с синтезированным алгоритмом управления показывает, что они далеки от оптимальных и хуже, чем при синтезе управления другими методами (слишком большое время регулирования при единичном ступенчатом воздействии и ошибка при гармоническом). Объясняется это тем, что параметры функций принадлежности выбирались достаточно произвольно, а в качестве входов регулятора использовалась только величина ошибки по положению. Естественно ни о какой оптимальности полученного регулятора не может идти и речи. Поэтому актуальной становится задача оптимизации нечеткого регулятора, с целью достижения им максимально возможных показателей качества управления. Т.е. стоит задача оптимизации целевой функции f(a₁,a₂…a_n), где a₁,a₂…a_n – коэффициенты, определяющие вид и характеристики нечеткого регулятора. Для оптимизации нечеткого регулятора воспользуемся блоком ANFIS из среды Matlab. Также одним из способов улучшения характеристик регулятора может являться увеличение числа его входов. Это сделает регулятор более гибким и улучшит его характеристики. Добавим еще одну входную лингвистическую переменную – скорость изменения входного сигнала (его производную). Соответственно возрастет и число правил. Тогда принципиальная схема регулятора примет вид:

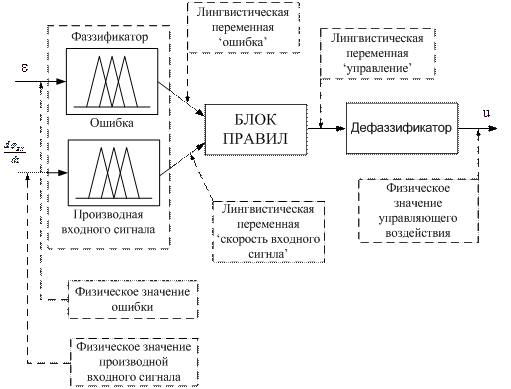
Рис.14 Принципиальная схема нечеткого регулятора с тремя лингвистическими переменными.

Пусть - значение скорости входного сигнала. Базовое терм-множество Тn определим в виде:

Тn={”отрицательная (ВО)”, “нулевая (Z)”, ”положительная (ВР)”}.

Расположение функций принадлежности для всех лингвистических переменных показано на рисунке.

Рис.15. Функции принадлежности лингвистической переменной «ошибка».

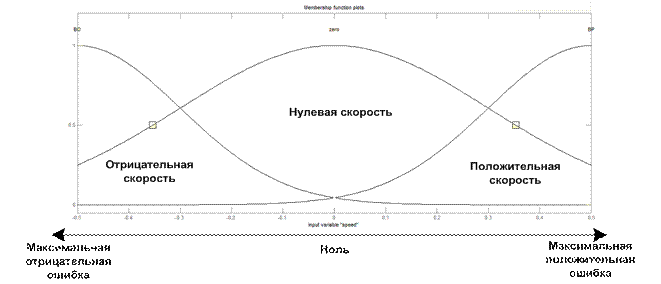
Рис.16. Функции принадлежности лингвистической переменной «скорость входного сигнала».

В связи с добавлением еще одной лингвистической переменной, количество правил возрастет до 3x5=15. Принцип их составления полностью аналогичен рассмотренному выше. Все они приведены в следующей таблице:

Таблица 3

Нечеткий сигнал управления	Ошибка по положению
BO	MO	Z	MP	BP
Скорость	BP	BO	BO	MO	MP	BP
Z	BO	MO	Z	MP	BP
BO	BO	MO	MP	BP	BP

Например, если если ошибка = нуль, а производная входного сигнала = большая положительная, то управляющее воздействие = малое отрицательное.

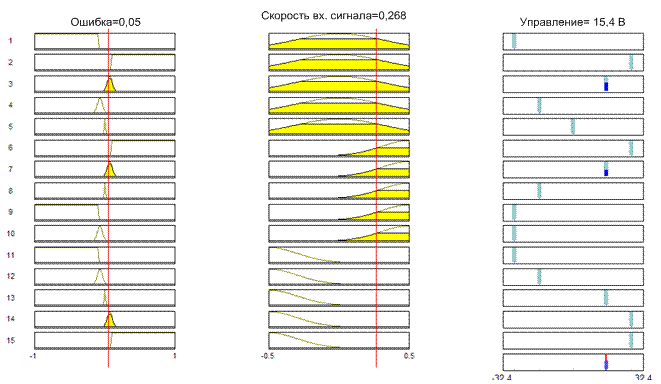Рис.17. Формирование управления при трех лингвистических переменных.

В связи с увеличением числа входов и соответственно самих правил, усложнится и структура нечеткого регулятора.

Рис.18. Структурная схема нечеткого регулятора с двумя входами.

Добавить рисунок

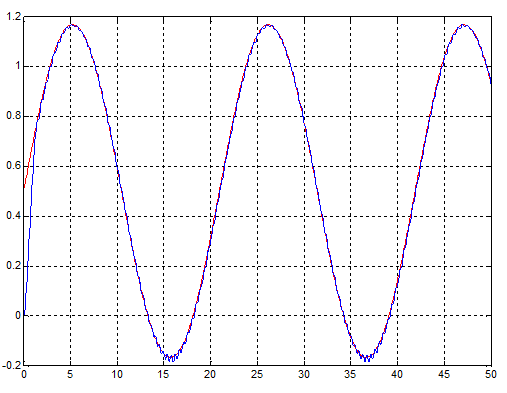
Рис.20. Переходный процесс при гармоническом входном воздействии для модели с нечетким регулятором, содержащим две входные лингвистические переменные.

Рис. 21. Сигнал ошибки при гармоническом входном воздействии для модели с нечетким регулятором, содержащим две входные лингвистические переменные.

Промоделируем работу нечеткого регулятора с двумя входами в среде Matlab. Структурная схема модели будет точно такой же, как на рис. 19. Из графика переходного процесса для гармонического входного воздействия можно видеть, что точность системы значительно возросла, но при этом увеличилась её колебательность, особенно в местах, где производная выходной координаты стремится к нулю. Очевидно, что причинами этого, как уже говорилось выше, является неоптимальный выбор параметров функций принадлежности, как для входных, так и для выходных лингвистических переменных. Поэтому оптимизируем нечеткий регулятор с помощью блока ANFISedit в среде Matlab.

Дата добавления: 2014-01-14