Основы теории зубчатого зацепления

При работе зубчатых колес зубья одного колеса входят во впадины другого (рис. 6.6), при этом боковая поверхность зуба ведущего колеса давит на боковую поверхность зуба ведомого колеса.

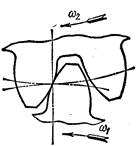
Рис. 6.6. Зубчатое зацепление

Профили зубьев пары колес должны быть сопряженными, т. е. заданному профилю зуба одного колеса должен соответствовать вполне определенный профиль зуба другого колеса. Чтобы обеспечить постоянство передаточного числа, профили зубьев нужно очертить такими кривыми, которые удовлетворяли бы требованиям основной теоремы зацепления.

Основная теорема зацепления. Для доказательства теоремы рассмотрим пару сопряженных зубьев в зацеплении (рис. 6.7). Профили зубьев шестерни и колеса касаются в точке S, называемой точкой зацепления. Центры вращения О₁ и О₂ расположены на неизменном расстоянии А друг от друга. Зуб шестерни, вращаясь с угловой скоростью ω₁ оказывает в точке S силовое действие на зуб колеса, сообщая последнему угловую скорость ω₂. Проведем через точку S общую для обоих профилей касательную ТТ и.нормаль NN. Окружные скорости точки S относительно центров вращения О₁ и О₂ будут v₁=O₁Sּ ω₁ и v₂=O₂Sּ ω₂.

Разложим v₁ и v₂ на составляющие v₁^΄ и v₂^΄ по направлению нормали NN и составляющие v₁΄΄ и v₂΄΄ по направлению касательной ТТ. Для обеспечения постоянного касания профилей необходимо соблюдение условия v₁^΄ = v₂^΄, в противном случае, при v₁^΄ < v₂^΄ зуб шестерни отстанет от зуба колеса, а при v₁^΄ > v₂^΄ произойдет врезание зубьев.

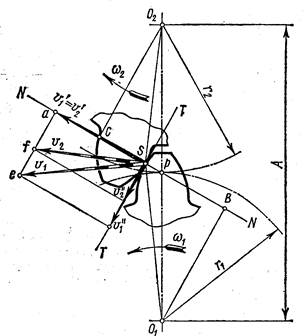
Рис. 6.7. Схема к доказательству основной теоремы зацепления

Опустим из центров О₁ и О₂ перпендикуляры О₁В и О₂С на нормаль NN. Из подобия треугольников aeS и BSO₁ v₁^΄/ v₁ = О₁В/O₁S, откуда

v₁^΄ = v₁· О₁В/O₁S = ω₁· О₁В.

Из подобия треугольников afS и CSO₂ v₂^΄/ v₂ = О₂C/O₂S, откуда

v₂^΄ = v₂· О₂C/O₂S = ω₂· О₂C.

Но v₁^΄ = v₂^΄, следовательно, ω₁· О₁В = ω₂· О₂C.

Отсюда передаточное число

i = ω₁/ ω₂= О₂C / О₁В.

Нормаль NN пересекает линию центров О₁О₂ в точке р, называемой полюсом зацепления. Из. подобия треугольников О₂рС и О₁pВ

О₂C / О₁В= О₂p / О₁p= r₂/r₁.

Сравнивая отношения (а) и (б), получаем:

i = ω₁/ ω₂=r₂/r₁ = const (6.1)

Таким образом, основная теорема зацепления формулируется следующим образом: для обеспечения постоянного передаточного числа зубчатых колес профили их зубьев должны очерчиваться по кривым, у которых общая нормаль NN, проведенная через точку касания профилей, делит расстояние между центрами O₁ и O₂, на части, обратно пропорциональные угловым скоростям.

Полюс зацепления р сохраняет неизменное положение на линии центров O₁ и O₂,следовательно, радиусы r₁ и r₂ также неизменны. Окружности радиусов r₁ и r₂ называют начальными. При вращении зубчатых колес начальные окружности перекатываются друг по другу без скольжения, о чем свидетельствует равенство их окружных скоростей ω₁r₁ = ω₂r₂ полученное из формулы (6.1).

Из множества кривых, удовлетворяющих требованиям основной теоремы зацепления, практическое применение в современном машиностроении получила эвольвента окружности, которая:

а) позволяет сравнительно просто и точно получить профиль зуба в процессе нарезания;

б) без нарушения правильности зацепления допускает некоторое изменение межосевого расстояния А (это изменение может возникнуть в результате неточностей изготовления и сборки).

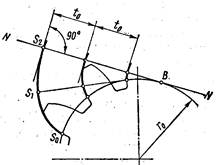
Рис. 6.8. Схема образования эвольвенты

Эвольвента окружности (рис. 6.8). Эвольвентой окружности называют кривую, которую описывает точка S прямой NN, перекатываемой без скольжения по окружности радиуса r_о. Эта окружность называется эволютой, или основной окружностью, а перекатываемая прямая NN — производящей прямой. Характер эвольвентного зубчатого зацепления определяется свойствами эвольвенты:

1. Производящая прямая NN является одновременно касательной к основной окружности и нормалью ко всем производимым ею эвольвентам.

2. Две эвольвенты одной и той же основной окружности эквидистантны. Эквидистантными (равноудаленными) называются две кривые, расстояние между которыми в направлении нормали везде одинаковое.

3. С увеличением радиуса r_о основной окружности эвольвента становится более пологой и при r_о→ ∞ обращается в прямую.

4. Радиус кривизны эвольвенты в точке S₂ равен длине дуги S₀В основной окружности. Центр кривизны эвольвенты в данной точке находится на основной окружности.

Контрольные вопросы

1. На рис. 6.1 и 6.5 определите направление вращения колес, если шестерни вращаются по часовой стрелке.

2. Какими достоинствами обладают зубчатые передачи?

3. В чем заключается различие открытых и закрытых зубчатых передач?

4., Какие основные требования предъявляют к профилям сопряженных зубьев?

5. Почему в современном машиностроении в основном применяют эвольвентное зацепление?

б. Как изменяется эвольвента с увеличением радиуса основной окружности?

Дополнительная литература

[121, лист 23.

[181, стр. 148, задача 9.9.

Дата добавления: 2014-01-14