Применение рядов Тейлора

Откуда

(9)

И т. д. После n - кратного дифференцирования получим

(10)

Подставим полученные данные в уравнение (1). Получим

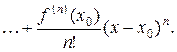(11)

Обозначим разность

(12)

Эта разность очевидно равна погрешности, которую мы получим при замене функции y=¦(x) многочленом P_n(x). Из формул (11) и (12) следует

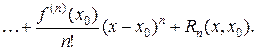(13)

Для оценки погрешности можно использовать разные формулы. Приведем без доказательства оценку погрешности в форме Лагранжа. Тогда при x>x₀ имеем

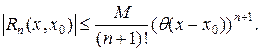(14)

где

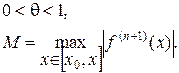
Наиболее часто формула Тейлора применяется для приближенных вычислений. В частном случае, когда x₀ =0, формула (13) называется формулой Маклорена.

Пусть функция y=f(x) бесконечно дифференцируема в в окрестности точки x=x₀. Перейдем формально к пределу при n®¥. Получим ряд, который называется рядом Тейлора

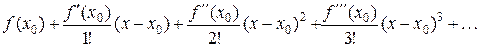
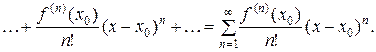(15)

В частном случае, когда x₀ =0, ряд (4) называется рядом Маклорена. Ряд (15) является степенным рядом. Пусть он сходится на некотором интервале. По свойствам степенных рядов его сумма является непрерывной функцией в этом интервале. Обозначим ее S(x). Однако может оказаться, что S(x)¹ f(x) в этом интервале.

Теорема. Для того чтобы ряд Тейлора сходился к функции f(x) необходимо и достаточно, чтобы

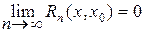
Без доказательства.

Для наиболее интересных для практики случаев ряд Тейлора сходится к функции, для которой он построен. Рассмотрим их в окрестности точки x₀=0.

Функция y=e^x

Найдем производные и их значения в точке x=0.

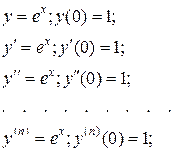
Тогда

Область сходимости (-¥;¥).

Аналогично строятся формулы Тейлора и для основных аналитических функций.

Приведем формулы Тейлора основных элементарных функций.

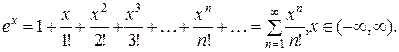
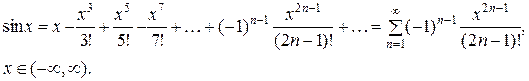
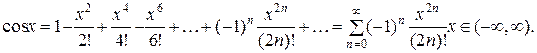
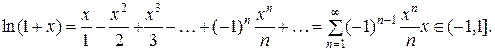
Вычислить значения функции y=e^x с заданной точностью. Положим x=1. Тогда оценка погрешности по формуле (14) дает

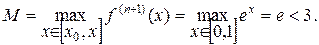
и

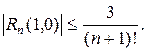
Для вычисления значения e с точностью e>0 достаточно взять такое n, чтобы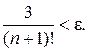

Так для вычисления e с точностью e=10^-8 достаточно взять n=9.

Дата добавления: 2014-01-14