Замена переменных в двойных интегралах. Часто при вычислениях двойных интегралов полезно применять замену переменных

Часто при вычислениях двойных интегралов полезно применять замену переменных. Рассмотрим прием замены на примере перехода к полярным координатам. Пусть задана прямоугольная декартова система координат Oxy. Выберем полюс в начале координат и полярную ось, проходящую по оси Ox. Точка M(x,y) в полярной системе имеет координаты M(r,j). Переход от полярной системы к декартовой формулой

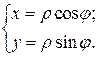(4)

Обратный переход

(5)

Пусть нам дан интеграл

y

b r=r₂(j)

a r=r₁(j)

x

Рис. 1. Разбиение области в полярных координатах

Перейдем к полярным координатам. Замена переменных дается формулой (4). Разобьем область (см. рис. 1) на элементарные площадки системой линий r=const, j=const. Система линий r=const задает систему концентрических окружностей с центром в начале координат, система линий j=const задает систему лучей, выходящих из начала координат. Обозначим систему линий r=r_i j=j_j и рассмотрим элементарную площадку. Очевидно, что

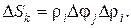
Получим

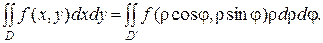
где область D¢ та же область D, но заданная в полярных координатах.

Для перехода к повторному интегралу проведем через каждую точку области D лучи, выходящие из начала координат. Множество концов лучей, входящих в область D, задают часть границы области, уравнение которой имеет вид r=r₁(j). Множество концов лучей, выходящих из области D, задают часть границы области, уравнение которой имеет вид r=r₂(j). Предельные положения лучей, проходящих через область, задают углы j=a и j=b. Тогда

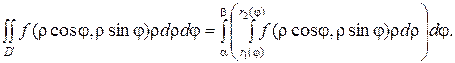
Пример. Вычислить интеграл

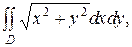
где D область, граница которой задана линией и условием

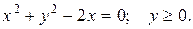
Изобразим область (см. рис. 2) и перейдем к полярным координатам

y

O x

Рис. 2. Область интегрирования для данной задачи

Получим

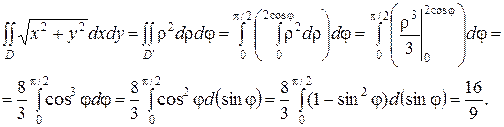
21.2. Тройные интегралы

Дата добавления: 2014-01-14