Определенного интеграла

Задачи, приводящие к понятию

1.Площадь криволинейной трапеции

Понятие определённого интеграла является одним из основных понятий математики. Между определённым и неопределённым интегралами существует тесная связь, которая и лежит в основе практического использования определённого интеграла.

К понятию определённого интеграла приводят многие задачи геометрии, механики и физики. Рассмотрим такую задачу.

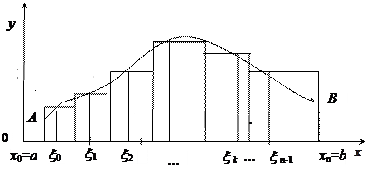Рис. 8.

Пусть функция y = f (x) непрерывна на отрезке [ a,b ], причём f (x) >0. Рассмотрим фигуру, ограниченную осью Ох, графиком y = f (x), и двумя прямыми: x = a и x = b.

Эта фигура называется криволинейной трапецией, отрезок [ a,b ] оси Ох – её основанием (рис. 8).

Найдём площадь этой фигуры. Разобьём отрезок [ a,b ] на n частей произвольным образом. Через точки деления х ₁, х ₂ ,…х_{n -1}проведем прямые, параллельные оси Оу. Криволинейная трапеция при этом разбивается на n частей. Обозначим длины элементарных отрезков через Δ х_k:

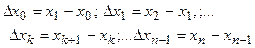В каждом из элементарных промежутков возьмём произвольную точку:

.

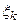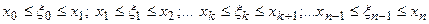Вычислим значения функции f (x) в этих точках:

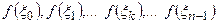
Каждую элементарную полоску с основанием 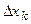заменим прямоугольником с тем же самым основанием 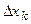и высотой f (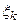) (k = 0, 1, 2,… n -1). Площадь каждого такого прямоугольника равна f (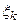) Δ х_k.

При этом криволинейная трапеция заменяется ступенчатой фигурой, площадь которой равна сумме площадей элементарных прямоугольников:

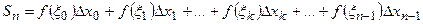или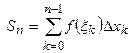

Ясно, что площадь S_n ступенчатой фигуры не равна площади криволинейной трапеции, а является лишь приближённым значением искомой площади. Очевидно, что это приближение будет тем более точным, чем меньше длина частичны интервалов (и больше n)

Если измельчать разбиение отрезка 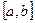, то число промежутков возрастает и полоски становятся уже, т.е. ломаная линия будет теснее примыкать к кривой .

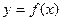За площадь криволинейной трапеции принимают предел, к которому стремиться S_n, когда разбиение отрезка 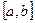делается сколь угодно мелким (если такой предел существует): 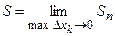или

(1)

Здесь 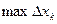- наибольшая длина элементарного отрезка.

Данное определение соответствует интуитивным представлениям о площади плоской фигуры и оно полностью оправдывается практикой.

Дата добавления: 2014-01-14