
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Несобственные интегралы. При определении интеграла предполагалось, что:
|
|
|
|
Лекция №22.
При определении интеграла 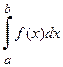 предполагалось, что:
предполагалось, что:
1. промежуток  конечен.
конечен.
2. функция f (x) определена и непрерывна в  (интегрируемость в смысле Коши)
(интегрируемость в смысле Коши)
Рассмотрим теперь интегралы, для которых эти условия нарушаются.
1. Интегралы с бесконечными пределами интегрирования (несобственные интегралы I рода).
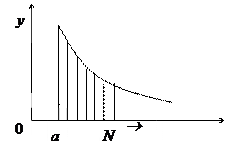
 .
.
 на n частей конечной длины.
на n частей конечной длины.
|
Рис. 19.
Тем не менее интегралы с бесконечными пределами встречаются как в математике, так и в приложениях. Однако это уже иные интегралы.
Рассмотрим f (x) на 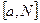 (рис. 19). Она интегрируема на этом отрезке:
(рис. 19). Она интегрируема на этом отрезке:
 . (14)
. (14)
Несобственным интегралом от функции f(x) по бесконечному промежутку  называют предел интеграла (14) при
называют предел интеграла (14) при 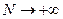 :
:
 .
.
Если предел существует, то несобственный интеграл называется сходящимся. Если предел не существует или бесконечен, то несобственный интеграл называется расходящимся.
Примеры.
1. 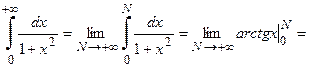

Интеграл сходится.
2. 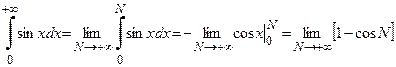
Предел не существует – интеграл расходится.
Часто бывает достаточно знать, сходится или расходится рассматриваемый несобственный интеграл.
Пусть  при
при  . Очевидно, что в этом случае интеграл
. Очевидно, что в этом случае интеграл 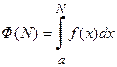 есть монотонно возрастающая функция от переменной N: большему значению N соответствует большее значение площади фигуры. Если при этом функция
есть монотонно возрастающая функция от переменной N: большему значению N соответствует большее значение площади фигуры. Если при этом функция 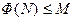 при
при 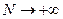 , (ограничена), то она имеет предел (признак существования предела):
, (ограничена), то она имеет предел (признак существования предела):
 , т.е.
, т.е. 
Интеграл сходится.
Если 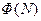 неограниченна при
неограниченна при  , то несобственный интеграл расходится к бесконечности:
, то несобственный интеграл расходится к бесконечности:  .
.
Теорема. Пусть для 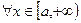 выполняется соотношение:
выполняется соотношение:
 , (15)
, (15)
тогда:
1. Если 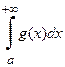 сходится, то сходится и
сходится, то сходится и  .
.
2. Если  расходится, то расходится и
расходится, то расходится и 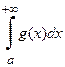 .
.
Следствие 1. Если f (x) непрерывна на , причём
, причём
 , где p >1, то
, где p >1, то  сходится.
сходится.
Следствие 2. Если f (x) непрерывна на  ,
,  и
и  , где
, где  , то
, то  расходится.
расходится.
Примеры.
1.Исследовать сходимость интеграла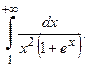
Сравним данный интеграл с известным сходящимся интегралом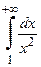 .
.
Так как при 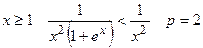 , то
, то  .
.
Следовательно интеграл сходится.
Несобственные интегралы от неограниченных функций (несобственные интегралы второго рода).
Непрерывная на отрезке функция интегрируема на нём.
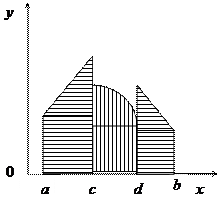 1. Пусть функция f (x) определена и непрерывна на конечном промежутке
1. Пусть функция f (x) определена и непрерывна на конечном промежутке  за исключением конечного числа точек. Если f (x) на отрезке
за исключением конечного числа точек. Если f (x) на отрезке  имеет конечное число только разрывов I рода (конечные скачки), то в этом случае отрезок
имеет конечное число только разрывов I рода (конечные скачки), то в этом случае отрезок  точками с и d можно разбить на три промежутка, в каждом из которых функция f (x) непрерывна. В этом случае интеграл в пределах от a до b на основании свойств аддитивности определяется как сумма
точками с и d можно разбить на три промежутка, в каждом из которых функция f (x) непрерывна. В этом случае интеграл в пределах от a до b на основании свойств аддитивности определяется как сумма
Рис.23 интегралов от непрерывных функций:
 (собственные интегралы).
(собственные интегралы).
2. Пусть функция f (x) определена и непрерывна при 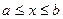 , а в точке b терпит бесконечный разрыв (разрыв II рода). В этом смысле определённый интеграл на
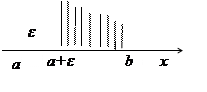
, а в точке b терпит бесконечный разрыв (разрыв II рода). В этом смысле определённый интеграл на  не может существовать, т.к. не существует предел интегральных сумм. Поступим следующим образом. Возьмём произвольное число
не может существовать, т.к. не существует предел интегральных сумм. Поступим следующим образом. Возьмём произвольное число  и рассмотрим отрезок
и рассмотрим отрезок  (рис. 24).
(рис. 24).
 |
Рис. 24.
Функция f (x) непрерывна на этом отрезке, значит существует интеграл 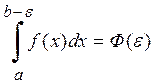 .
.
Если существует предел этого интеграла когда 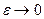 , то этот предел называется несобственным интегралом второго рода и обозначается:
, то этот предел называется несобственным интегралом второго рода и обозначается:
 .
.
Если предел не существует или бесконечен, то несобственный интеграл называется расходящимся.
Аналогично определяется интеграл с особенностью на нижнем пределе.
Пусть f (x) непрерывна на  , а при х=а имеет разрыв второго рода (рис. 25), тогда
, а при х=а имеет разрыв второго рода (рис. 25), тогда

|




|
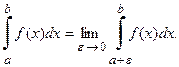 .
.
 | |||||||||||
 | |||||||||||
Рис. 25.
Пусть функция f (x) на отрезке  имеет несколько точек разрыва второго рода (рис. 27). Тогда промежуток разбивают на частичные так, чтобы на каждом из них было по одной точке разрыва, расположенной на конце интервала:
имеет несколько точек разрыва второго рода (рис. 27). Тогда промежуток разбивают на частичные так, чтобы на каждом из них было по одной точке разрыва, расположенной на конце интервала:

Если все интегралы в правой части сходятся, то сходится и интеграл в левой части. Если хотя бы один из интегралов справа расходится, то расходится и интеграл, стоящий справа.
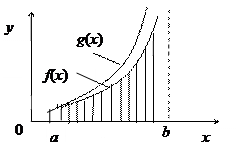
Теорема: Пусть 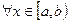 выполнено условие
выполнено условие  , причём f (x) и g (x) непрерывны при
, причём f (x) и g (x) непрерывны при 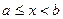 , а при x=b имеют бесконечные разрывы. Тогда:
, а при x=b имеют бесконечные разрывы. Тогда:
1. Если 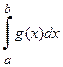 сходится, то сходится и
сходится, то сходится и 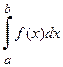 ;
;
2.  Если
Если 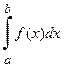 расходится, то расходится и
расходится, то расходится и 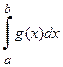 .
.
Рис. 28.
Следствие 1. Если  и p <1, то
и p <1, то 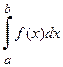 сходится.
сходится.
Следствие 2. Если  , непрерывна при
, непрерывна при 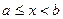 , а при x=b имеет разрыв первого рода и
, а при x=b имеет разрыв первого рода и  , где
, где 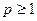 , то
, то 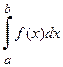 расходится.
расходится.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 458; Нарушение авторских прав?; Мы поможем в написании вашей работы!