Площадь криволинейного сектора в полярной системе координат

Площадь плоской фигуры в декартовых координатах

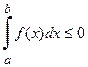Если на отрезке , то площадь криволинейной трапеции вычисляют по формуле (1). Если на , то и

S= -

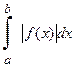
Если f (x) принимает на значения разных знаков, то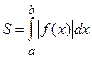

1. Полярные координаты

Декартовы координаты – не единственный способ определять положение точки. Существует много типов координатных систем. Наиболее употребительной (после декартовой) системой координат на плоскости является полярная.

Возьмём на плоскости точку О, которую назовём полюсом. Проведём луч ОР – полярную ось. Выберем единицу масштаба. Возьмём на плоскости произвольную точку

Рис. 36. Рис. 37.

М и соединим её с полюсом (рис. 36). Полярными координатами точки М называются числа и : - полярный радиус точки М, - её полярный угол: . Очевидно, что .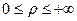

Если угол отсчитывать против часовой стрелки (положительные значения), то достаточно рассматривать его значения в промежутке . Иногда приходится рассматривать углы больше, чем . Иногда наряду с положительными, рассматривают и отрицательны: .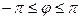

При таком соглашении каждой точке на плоскости (кроме полюса) соответствует единственная пара чисел . Для полюса полярный угол не определён.

2. Связь декартовых координат с полярными.

Совместим с полярной системой координат декартову так, чтобы её начало совпало с полюсом, а ось Ох с полярной осью; - полярные координаты точки М, а (х,у) – её декартовы координаты.

Из треугольника:

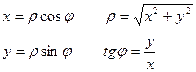(3)

Получили формулы перехода от полярной системы координат к декартовым и наоборот.

Как и в случае декартовой системы координат, всякой кривой можно поставить в соответствии её уравнение в полярной системе координат: .

3. Площадь в полярных координатах.

Пусть линия задана уравнением 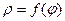. Найдём площадь криволинейного сектора, ограниченного данной линией и двумя лучами: и , выходящими из полюса.

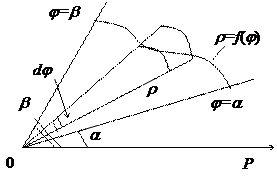Возьмём произвольное значение и увеличим угол на бесконечно малую величину . Тогда к площади добавится бесконечно малый криволинейный сектор (рис.41):

Рис. 41.

. (4)

Дата добавления: 2014-01-14