
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула трапеций. Как и в предыдущем случае, делим отрезок на n равных частей:
|
|
|
|
Как и в предыдущем случае, делим отрезок  на n равных частей:
на n равных частей: 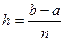 . Каждую элементарную дугу заменим соответствующей хордой, в результате чего криволинейная трапеция заменяется суммой площадей элементарных прямоугольных трапеций. Геометрически очевидно, что такие трапеции более точно выражает искомую площадь, чем прямоугольники. Площадь каждой элементарной трапеции равна:
. Каждую элементарную дугу заменим соответствующей хордой, в результате чего криволинейная трапеция заменяется суммой площадей элементарных прямоугольных трапеций. Геометрически очевидно, что такие трапеции более точно выражает искомую площадь, чем прямоугольники. Площадь каждой элементарной трапеции равна:
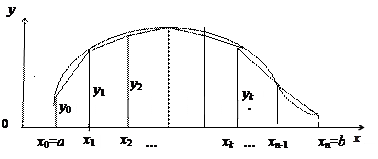 |
Рис. 51.
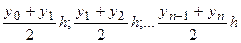 .
.
Складывая элементарные площади, получим:
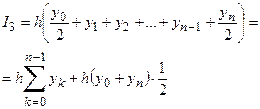 ,
, 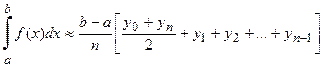 (4)
(4)
Полученная формула называется формулой трапеций.
Можно доказать, что если на  существует ограниченная производная
существует ограниченная производная 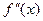 , то ошибка оценивается формулой:
, то ошибка оценивается формулой:
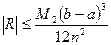 , т.е.
, т.е. 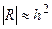 . Здесь М2 – наибольшее значение
. Здесь М2 – наибольшее значение 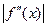 на
на  .
.
Формула парабол (формула Симпсона)
Ещё большая точность получается, если элементарные криволинейные трапеции заменить параболическими трапециями.
Разобьём отрезок [ a, b ]на чётное число 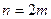 равных частей. Шаг разбиения при этом
равных частей. Шаг разбиения при этом 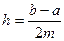 и вычислим значения функции f (x) в точках деления:
и вычислим значения функции f (x) в точках деления: 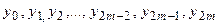 . Рассмотрим n троек точек деления на кривой y = f (x):
. Рассмотрим n троек точек деления на кривой y = f (x): 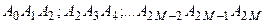 . Через всякие три точки, не лежащие на одной прямой, можно провести единственную параболу второй степени:
. Через всякие три точки, не лежащие на одной прямой, можно провести единственную параболу второй степени:
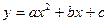 (5)
(5)
Через выделенные тройки точек проведём параболы с осями, параллельными оси Оу. Площадь элементарной криволинейной трапеции заменится площадью элементарной параболической трапеции. Вычислим площадь такой трапеции.
Лемма: Площадь параболической трапеции с основанием 2 h равна: 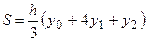 , где
, где 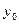 и
и  - ординаты кривой в крайних точках, а
- ординаты кривой в крайних точках, а 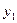 - ордината кривой в середине отрезка.
- ордината кривой в середине отрезка.
Приближённое значение интеграла:
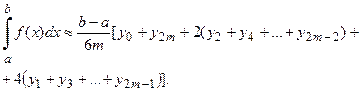
Полученная формула носит название формулы Симпсона.
Если существует ограниченная 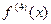 на
на  , то погрешность формулы Симпсона оценивается следующим образом:
, то погрешность формулы Симпсона оценивается следующим образом:  , т.е.
, т.е.  . Здесь
. Здесь 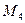 - наибольшее значение
- наибольшее значение  на отрезке
на отрезке  .
.
Все рассмотренные формулы тем точнее, чем больше n: 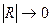 при
при 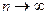 . При одном и том же n формула Симпсона – наиболее точная из них.
. При одном и том же n формула Симпсона – наиболее точная из них.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 491; Нарушение авторских прав?; Мы поможем в написании вашей работы!