Оператор Гамильтона. Для упрощения работы с введенными понятиями Гамильтон ввел символический оператор Ñ, равный

Для упрощения работы с введенными понятиями Гамильтон ввел символический оператор Ñ, равный

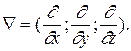
Оператор называется набла.

С помощью введенного оператора запишем

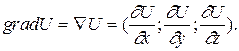
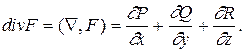
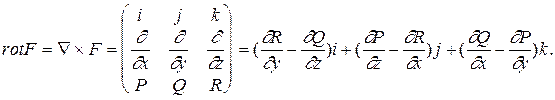
Теорема. Для того чтобы поле F было потенциальным, необходимо и достаточно, чтобы rot F= 0.

Доказательство. Необходимость. Пусть поле потенциально. Это значит, что существует потенциал U=U(x,y,z) такой, что F = gradU. Тогда

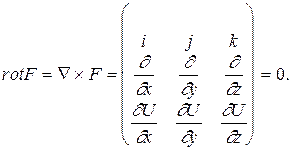
Достаточность. Пусть rot F= 0. Тогда

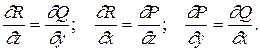
Это значит интеграл по контуру в области не зависит от вида контура, а зависит только от начала M₀(x₀,y₀,z₀) и конца M(x,y,z) контура. Поэтому запишем

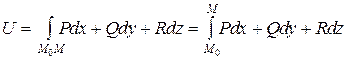
Найдем производную. Получим

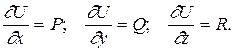
Это значит, что

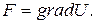
Теорема Остроградского-Гаусса и теорема Стокса являются наиболее используемыми теоремами теории поля. Поэтому сформулируем их еще раз в новых терминах

Теорема Остроградского-Гаусса. Пусть в некоторой области D трехмерного пространства задано векторное поле F.

F =P(x,y,z) i+Q (x,y,z) j+R (x,y,z) k = (P(x,y,z);Q(x,y,z);R(x,y,z)).

пусть S - замкнутая поверхность, лежащая в области D, V - тело, ограниченное поверхностью S. Если функции непрерывны и имеют непрерывные частные производные, то поток векторного поля через поверхность S равен интегралу по объему от дивиргенции F

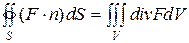
Интеграл берется по внешней стороне поверхности.

Разделим обе части равенства на V и перейдем к пределу при V ®0. Получим

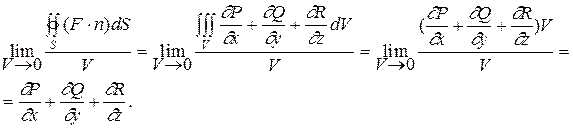
Для случая поля скоростей течения жидкости поток равен количеству жидкости, протекающей через поверхность S. Если он равен нулю, то количество втекающей жидкости равно количеству вытекающей. Если поток равен нулю для любого объема, то жидкость внутри объема не появляется и не исчезает. Это соответствует случаю дивергенции, равному нулю. Если поток через замкнутую поверхность больше нуля, то это означает, что внутри поверхности имеется источник жидкости. Поэтому дивергенция характеризует мощность источников жидкости в данной точке поля.

Теорема Стокса. Пусть в некоторой области D трехмерного пространства задано векторное поле F.

F =P(x,y,z) i+Q (x,y,z) j+R (x,y,z) k = (P(x,y,z);Q(x,y,z);R(x,y,z)).

Пусть L замкнутый контур, лежащий в области D, S - некоторая поверхность, натянутая на контур L. Поверхность S лежит в области D. Направление обхода контура и выбор стороны поверхности согласованы по следующему правилу: если двигаться по направлению обхода контура так, чтобы поверхность оставалась с левой стороны, то нормаль к поверхности проходит от ног к голове. Если функции непрерывны и имеют в области D непрерывные частные производные, то циркуляция по контуру равна потоку ротора через поверхность S

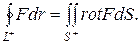
Разделим обе части равенства на S и перейдем к пределу при S ®0. Получим

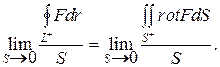
Из теоремы Стокса следует, что

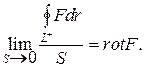
Ротор F показывает величину завихренностиполя.

Дата добавления: 2014-01-14