Криволинейный интеграл

Применение кратных интегралов.

Двойной интеграл применяется для вычисления расстояния, объёма и т. д.:

;

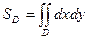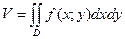
Тройной интеграл применяется для вычисления момента инерции тела, координат центра тяжести, объёма тела:

Пусть AB – гладкая дуга на которой определена непрерывная векторная функция.

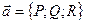; . Векторная функция – вектор, зависящий от функций, из которых он исходит. Разобьём дугу АВ на n-элементарных частей.

. Выберем 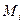на каждом элементарном кусочке и составим элементарную формулу:

Конечный предел составленных интегрированных сумм 0. Он называется криволинейным интегралом векторной функции A(M) по дуге AB. Если дуга 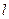замкнута, то говорят о криволинейном интеграле . Обход замкнутого контура против часовой стрелки считается положительным.

Свойства криволинейного интеграла:

1. Если изменить направление обхода дуги АВ, то криволинейный интеграл изменит знак:

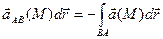
2. Интеграл от суммы векторной функции равен сумме интегралов каждой из них:

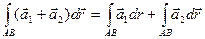
3.

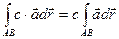
4. Если путь интегрирования разбит на конечное число частей, то интеграл по всему пути равен сумме интегралов по всем его частям:

Если область D, ограниченную замкнутой линией 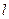, разбить на и , то криволинейный интеграл по всей линии равен сумме интегралов, взятых в том же направлении по линиям и 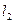, ограничивающим области.

Алгоритм вычисления криволинейного интеграла:

1. Составить параметрические уравнения дуги АВ и установить пределы изменения параметра Т; .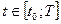

2. Выполнить замену переменных: ; ; ; ; ;

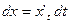и преобразовать криволинейный интеграл по дуге АВ в определённый интеграл по 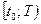. Пример:

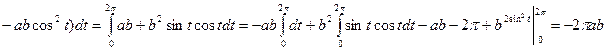
L-эллипс, ограниченный x=acost; y=bsint

;

; ;

;

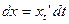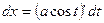
Дата добавления: 2014-01-14