Необходимое условие сходимости ряда. При исследовании рядов на сходимость возникают две задачи исследовать ряд на сходимость, зная что ряд сходится найти его сумму

При исследовании рядов на сходимость возникают две задачи исследовать ряд на сходимость, зная что ряд сходится найти его сумму.

Теорема (необходимое условие сходимости ряда).

Если ряд сходится то его общий член стремится к 0 то есть 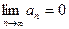(7)

Замечание: условие (7) является необходимым но не является достаточным условием сходимости ряда.

Таким образом, если общий член ряда стремится к 0 то еще нельзя сделать вывод о сходимость ряда, необходимо дополнительное исследование с помощью других признаков сходимости ряда.

Замечание: Если для некоторого ряда а_n не стремится к 0 то ряд расходится.

Дата добавления: 2014-01-14