Алгебраические операции над событиями

Случайные события

Прежде чем дать общее определение случайного события, рассмотрим частный случай. В приведенном выше примере 2 можно рассматривать событие, состоящее в том, что выпало четное число очков. Очевидно, что это событие А происходит только в том случае, когда осуществилось одно из трех элементарных событий ω₂, ω₄, ω₆, то есть А = {ω₂, ω₄, ω₆} есть часть множества Ω, его подмножество.

Пусть теперь Ω - произвольное пространство элементарных событий. Случайным событием (или просто событием) будем называть всякое подмножество пространства элементарных событий. С этой точки зрения элементарные события – это одноэлементные подмножества множества Ω. Случайные события будем обозначать в дальнейшем большими латинскими буквами А,В,С,....

Невозможным событием называется событие, совпадающее с пустым множеством пространства элементарных событий, и обозначается символом Ø. Другими словами невозможным называется событие, которое не может произойти в результате опыта.

Достоверным событием называется событие, совпадающее со всем элементарным пространством элементарных событий Ω. Иначе, достоверным называется событие, которое обязательно происходит в результате опыта.

События А и В называются равными (равносильными) А = В, если они состоят из одних и тех же элементарных событий.

Событие В есть следствие события А, если содержит все элементарные события, входящие в А, другими словами, если В происходит всякий раз, когда произошло А. Обозначается этот факт так А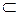В.

Суммой двух событий А и В одного и того же пространства элементарных событий Ω называется событие А + В (А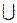В), состоящее из всех элементарных событий, принадлежащих по крайней мере одному из событий А или В. Другими словами, событие А + В состоит в том, что в реальном опыте произошло либо событие А, либо В, либо и то, и другое.

Произведением событий А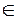Ω и В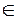Ω называется событие А·В (А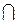В), состоящее из элементарных событий, принадлежащих и А, и В. Другими словами событие АВ происходит тогда и только тогда, когда происходит и событие А, и событие В.

Разностью событий А и В называется событие АB, состоящее из элементарных событий, принадлежащих А и не принадлежащих В.

На описательном языке это означает, что событие А произошло, а событие В не произошло,

Событие 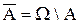называется противоположным событию А. События А и называются взаимно противоположными, так как А = .

При доказательстве некоторых утверждений в алгебре событий полезной оказывается геометрическая иллюстрация событий, трактуемых как попадание точки в область, соответствующую событию. Условно изображая события в виде различных областей на плоскости, получаем так называемые диаграммы Венна. Приведем их для введенных операций.

Заметим, что понятия суммы и произведения двух событий обобщаются на любое (в том числе и бесконечное) число событий. В этом случае пишут:

,

.

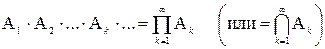Используя приведенные выше определения, легко доказать, что операции сложения, умножения и перехода к противоположному событию обладают следующими свойствами:

1. А+В=В+А А·В-В·А - коммутативность;

2. (А+В)+С=А+(В+С) (А·В)·С=А·(В·С) - ассоциативность;

3. (А+В)·С=А·С+В·С - дистрибутивность умножения относительно сложения.

Кроме этих трех основных свойств алгебраических операций отметим следующие (доказатъ самим):

А+А=А, АА=А, А+Ø=А, АØ=Ø, А+Ω=Ω, АΩ=А.

При решении задач часто оказываются полезными следующие равенства (доказать самим):

(правило де Моргана)

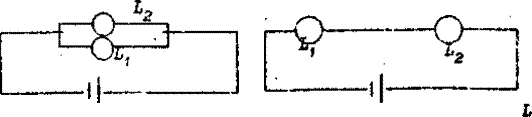
Пример использования алгебраических операций над событиями. Пусть имеются две электрические цепи

Обозначим через А событие, состоящее в том, что светится лампочка L₁, В – светится лапочка L₂, С – в цепи течет ток. Тогда для первой цепи С=А+В, для второй С=АВ.

События А и В, принадлежащие Ω, называются несовместными, если АВ=Ø. Другими словами, события А и В несовместны, если они не имеют общих элементарных событий.

Пример. Записать сумму А+В событий А и В в виде суммы двух несовместных событий.

Решение. Пусть 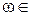А+В. Это означает, что или 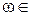А, или 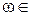В и не принадлежит А, то есть . Отсюда 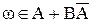и, следовательно, А+В= А+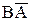. Аналогично показывается: из того, что 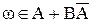следует, что .

Дата добавления: 2014-01-14