Лекция 4. Тема: Частные случаи уравнения сохранения энергии

Тема: Частные случаи уравнения сохранения энергии. Уравнение баланса механической энергии (уравнение Бернулли).

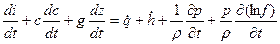. (1)

Энтальпия – мера работы; удельная энтальпия – некая удельная работа. Работа, совершаемая в единицу времени – мощность. Таким образом, полученное уравнение энергии записано «в мощностях»:

- удельная мощность, - удельная мощность, соответствующая кинетической энергии,

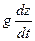- удельная мощность, соответствующая работе силы тяжести в поле земного тяготения,

- подводимые извне мощности, соответствующие теплоте и работе.

Рассмотрим важные частные случаи уравнения энергии.

Как правило, в нашем курсе рассматриваются простейшие случаи течения.

1. Стационарное движение.

С течением времени в данной точке пространства ничего не меняется.

, .

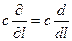Перепишем (1) с учетом записанных выше преобразований:

.

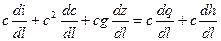Разделим все члены уравнения на скорость (это можно делать, если скорость не равна нулю, но нулевая скорость – это статика, которая нас сейчас не интересует). Избавимся также от в знаменателе.

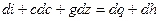(2)

В дальнейшем будем использовать именно уравнение энергии для стационарного случая (2).

Кроме того, обычно будем применять (2) при рассмотрении движения газов. При небольших перепадах высот потенциальная энергия у газов почти не изменяется, поэтому слагаемым для газовых потоков обычно пренебрегают.

1. .
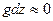2. Обычно рассматриваются адиабатические течения без подвода механической энергии:

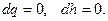
Чтобы избежать путаницы с терминологией, отметим, что в газовой динамике, говоря об адиабатном течении, подразумевают 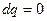и , и , тогда как в термодинамике термин «адиабатное течение» означает только отсутствие теплообмена .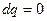

С учетом всех сделанных упрощений, получаем уравнение энергии в виде:

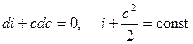. (3)

Определим физический смысл : если скорость потока равна нулю, то энтальпия принимает максимальное значение: - энтальпия торможения (энтальпия заторможенного потока) или полная энтальпия.

Таким образом, для стационарного адиабатического движения газа уравнение энергии записывается в форме

(4)

Физический смысл полученного уравнения: у газового потока внутренняя энергия связана с кинетической; если газ ускоряется, то, при отсутствии подвода энергии извне, он остывает, расходуя на разгон запасы своей внутренней энергии (). Напротив, при торможении поток разогревается ().

Принципиально важно отметить, что в процессе вывода соотношений (1) – (4) мы ничего не говорили о трении (в том числе о внутреннем трении в жидкостях – вязкости). Поэтому полученные уравнения пригодны в том числе и для течений с трением, по крайней мере в приближении одномерного движения, а не только для идеальной жидкости.

При наличии трения часть механической работы необратимо превращается в теплоту трения. Убыль механической работы на трение равна прибыли теплоты трения (и равны по модулю и противоположны по знаку). Можно добавить в правую часть уравнения (1) эти слагаемые, но они взаимно компенсируют друг друга.

Дата добавления: 2014-01-14