Уравнение Бернулли)

Уравнение баланса механической энергии для одномерного движения

Это уравнение выражает закон сохранения количества движения.

Идея вывода заключается в том, чтобы при помощи первого начала термодинамики исключить из уравнения энергии (1) .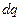

Существуют две распространенные формы записи первого начала, через внутреннюю энергию и через энтальпию:

.

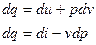Воспользуемся второй формой записи, используя вместо удельного объема плотность:

(*)

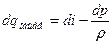Термодинамика делит все процессы на обратимые и необратимые.

Простейшая термодинамика – равновесная, рассматривающая предельное состояние бесконечно медленного (то есть по сути статику) и поэтому обратимого процесса.

В термодинамике рассматривают два вида необратимости:

1) внутреннюю, связанную с наличием трения в потоке,

2) внешнюю, возникающую при наличии конечной разности температур между потоком и горячим источником (если поток греем) или холодным источником (если поток охлаждаем).

Так как мы, в основном, рассматриваем адиабатные течения без теплообмена, второй вид необратимости нас не очень интересует. Остается необратимость, связанная с трением, с вязкостью.

Если в нашем рассмотрении силу, действующую на поверхности объема, моделировать давлением, и считать, что с двух сторон поверхности раздела давление одинаково, то при этом не учитывается трение.

Тогда, чтобы адекватно описывать течения с трением, запишем общее количество теплоты как сумму двух слагаемых:

, (**)

где первое слагаемое справа -внешняя теплота.

Переходим к записи в удельных мощностях, выражая удельную мощность сил трения через теплоту трения:

(***)

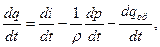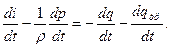(2)

Вычитаем из уравнения энергии (1) первое начало термодинамики в форме (2), чтобы получить баланс механической энергии:

-

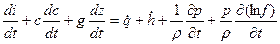
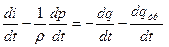
Заменяем теплоту трения на работу сил трения и получаем окончательно уравнение баланса механической

энергии:

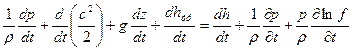
(3)

Первое слагаемое справа представляет собой мощность работы внешних сил, последнее слагаемое справа - мощность работы пульсации стенок струи.

Бернулли вывел это уравнение для случая стационарного движения :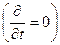

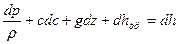. (4)

В простейшем случае, когда отсутствует работа внешних сил, получим

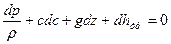. (5)

1) Для несжимаемой жидкости (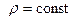) это уравнение легко интегрируется:

.

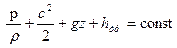Полученное выражение часто называют интегралом Бернулли.

Все слагаемые в этом интеграле имеют размерность удельной работы, таким образом, сумма работы сил давления, кинетической и потенциальной энергий и работы сил трения (для единичной массы) вдоль направления движения для стационарного режима при отсутствии внешних сил не меняется.

Поделив все члены на ускорение свободного падения, можно записать интеграл Бернулли через удельный вес :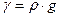

.

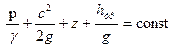Читается так: сумма пьезометрической высоты (пьезометрического напора), динамического напора, нивелирной высоты и напора трения вдоль потока для стационарного режима при отсутствии внешних сил постоянна.

2) Сжимаемая жидкость (газ), .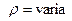

Пренебрегаем потенциальной энергией: .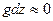

.

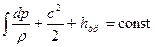Если отсутствует трение, то для газа дифференциальная форма уравнения Бернулли:

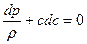(при этом теплообмен в потоке может присутствовать, это учтено в уравнении энергии).

Чтобы можно было посчитать интеграл 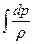, представляющий из себя по сути техническую работу, взятую с обратным знаком, необходимо, чтобы плотность была функцией только давления: 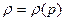. Такая связь плотности с давлением (или давления с плотностью) называется условиями баротропности.

С точки зрения термодинамики связь 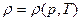- уравнение состояния, 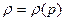- уравнение процесса. Знание условий баротропности равносильно знанию уравнения процесса.

Если задана зависимость 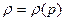, то 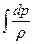берется и называется функцией давления .

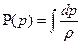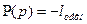. Функция давления определяется с точностью до определенной постоянной.

Через функцию давления интеграл Бернулли для сжимаемого газа записывается так:

.

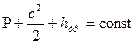Дата добавления: 2014-01-14