Закон равномерной плотности

Простейшие законы распределения.

При решении эконометрических задач приходится сталкиваться с различными распределениями случайных величин. Рассмотрим наиболее часто встречающиеся законы распределения.

На практике встречаются непрерывные случайные величины, о кото­рых заранее известно, что их возможные значения лежат в пределах неко­торого определенного интервала. Кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). О таких слу­чайных величинах говорят, что они распределяются по закону равномер­ной плотности.

Например, пусть поезда метрополитена идут с интервалом 4 мин. Пассажир выходит на платформу в некоторый момент времени. Время Т, в течение которого ему придется ждать поезда, представляет собой вели­чину, распределенную с равномерной плотностью на участке [0 - 4] ми­нут.

Плотность распределения для случайной величины X, распределенной на участке [а,b] по закону равномерной плотности, выражается соотно­шением:

Функция распределения F(x) имеет вид:

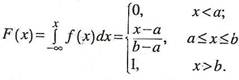
Определим основные числовые характеристики равномерного закона. Математическое ожидание

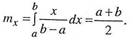
В силу симметричности равномерного распределения медиана величины Х также равна

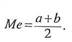
Моды закон равномерной плотности не имеет.

Дисперсия и среднее квадратическое отклонение определяются фор­мулами:

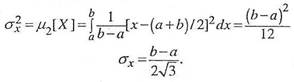
В силу симметричности распределения его асимметрия равна нулю.

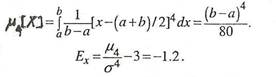
2. Биномиальный закон. Закон Пуассона

Биномиальным называют закон распределения дискретной случай­ной величины Х - числа появлений события в п независимых испытаниях, в каждом из которых вероятность появления события постоянна и равна р (вероятность непоявления события также постоянна и равна q=1 - р). При этом вероятность возможного значения X = m, где m - число появлений события в n испытаниях, вычисляется по формуле Бернулли:

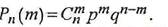
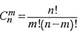
Здесь - число сочетаний из п элементов по m элементов.

Если в условиях биномиального закона число испытаний п велико, а вероятность р появления события в каждом испытании мала, то

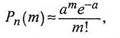
где т - число появлений события в п независимых испытаниях; а = пр.

В этом случае говорят, что дискретная случайная величина распре­делена по закону Пуассона.

Для закона Пуассона справедливо соотношение m_x = σ_x² = a

Типичная задача, приводящая к распределению Пуассона, заключает­ся в следующем. Пусть на оси х случайным образом распределяются точ­ки. Допустим, что случайное распределение точек удовлетворяет следую­щим условиям:

1. Вероятность попадания того или иного числа точек на отрезок ∆х зависит только от длины этого отрезка, но не зависит от его положения на оси, то есть точки распределены на оси с одинаковой средней плотностью (интенсивностью) λ (математическое ожидание числа точек, приходя­щихся на единицу длины, равно λ).

2. Точки распределяются на оси независимо друг от друга, то есть ве­роятность попадания того или иного числа точек на заданный отрезок не зависит от того, сколько их попало на любой другой отрезок, не перекры­вающийся с ним.

3. Вероятность попадания на малый участок ∆х двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек).

Исходя из этих условий можно доказать, что число точек, попадаю­щих на заданный отрезок длины ∆х на оси х, подчиняется закону распре­деления Пуассона, где а = λ∆х. Величина а по смыслу представляет собой среднее число точек, приходящееся на отрезок ∆х.

Распределение Пуассона возникает там, где какие-то точки (или дру­гие элементы) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек, попавших в заданную область.

Закон Пуассона часто называют, законом редких явлений из-за свой­ства выражать биномиальное распределение при большом числе опытов и малой вероятности события.

На практике часто при решении вопроса о принятии закона Пуассона для описания какой-то случайной величины определяют из опыта ее математическое ожидание и дисперсию. Если их значения близки, то это может служить в пользу гипотезы о пуассоновском распределении. Резкое различие этих характеристик, напротив, свидетельствует против этой гипотезы.

Пример. Брокеру поступают заявки на операции с ценными бума­гами со средней плотностью 15 заявок в час. Определить вероятность то­го, что за две минуты брокеру поступит: 1) ровно три заявки; 2) хотя бы одна заявка.

Решение. Считаем, что число заявок на любом участке времени распределено по закону Пуассона.

Среднее число заявок за две минуты a = 2 · 15 / 60 = 0,5.

Тогда вероятность поступления ровно трех заявок равна

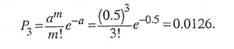
Вероятность того, что поступит хотя бы одна заявка за две минуты, равна

P₁ = 1 – P₀ = 1 – e^-0,5 = 1 – 0,606 = 0,394.

Дата добавления: 2014-01-14