Бесконечно большие последовательности

Тема: Бесконечно большие последовательности.

а_n=(-1)ⁿ – не имеет предел.

{b_n}={1,1…}

{a_n}={-1;1;-1;1…} – предел не существует.

a_n=2ⁿ

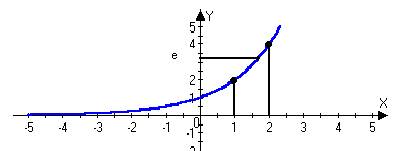
$N:"n>N Þ a_n>ε

b_n=(-1)ⁿ2ⁿ

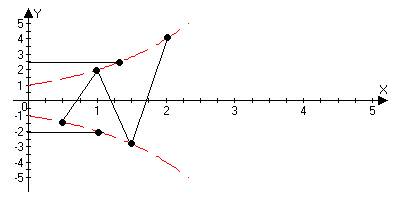
$N:"n>N Þ |b_n|>ε

c_n=-2ⁿ

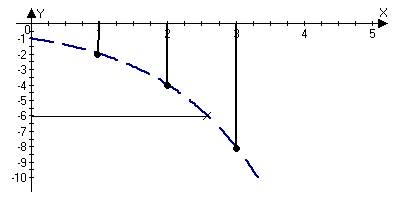
$N:"n>N Þc_n<-ε

Определение (бесконечно большие последовательности)

1) lim a_n=+¥, если "ε>0$N:"n>N Þ a_n>ε где ε- сколь угодно малое.

^n®¥

2)lim a_n=-¥, если "ε>0 $N:"n>N Þ a_n<-ε

^n®+¥

3) lim a_n=¥ Û "ε>0 $N:"n>N Þ |a_n|>ε

^n®+¥

Последовательностью имеющий конечный предел называют сходящимися. В противном случае последовательность называют расходящимися. Среди них есть последовательности, которые расходятся в бесконечность. О них мы говорим, что они имеют бесконечный предел.

Доказательство:

a_n=2ⁿ

Берём "ε>0; хотим 2ⁿ>ε

n>log₂ε

N=[log₂ε]+1

Правило формирования обратного утверждения: нужно поменять местами значки " и $, а знак неравенства на дополнительный.

Пример:

Утверждение lim a_n=a<¥ $aÎ R "ε>0 $NÎ N:"n> N Þ |a_n-a|<ε

^n®¥

Обратное утверждение "aÎ R $ε>0 "NÎ N:$ n> N Þ |a_n-a|<ε

Всякая бесконечно большая не ограниченная. Обратное утверждение неверно.

b_n{2;0;2ⁿ;0;2³;0….}

Теорема (об ограниченной сходящейся последовательности)

Пусть $lim a_n=a<¥ Þ a_n - ограниченная

^n®+¥

Доказательство:

Дано:

"ε>0$N:"n>N Þ |a_n-a|<ε

Раз "ε>0 возьмем ε=1 Þ $N:"n>N Þ |a_n-a|<1

a-1<a_n<1+a, "n>N

Этому неравенству может быть не удовлетворять только первые N члены последовательности.

N₁=max{|a₁|;|a₂|;…|a_n|;|1+a|;|a-1|}

a_n£c, "n> N

Теорема (о единстве предела сходящейся последовательности).

Если $lim a_n=a <¥, то а- единственное.

^n®+¥

Доказательство:(от противного)

Предположим, что $ b: lim a_n=b и b¹a ε=b-a/2>0 для определенности пусть b>a Þ$N₁:"n>N₁Þ |a_n-a|<ε

^n®+¥

$N₂:"n>N₂ Þ |a_n-b|<ε N=max{N₁;N₂}, тогда оба неравенства выполняются одновременно Þ

Þ -(b-a)/2<a_n-a<(b-a)/2

-(b-a)/2<a_n-b<(b-a)/2

a_n-a<(b-a)/2

-

a_n-b>-(b-a)/2

b-a<b-a

0<0 – противоречие Þ предположение, что b>a неверно. Аналогично доказывается, что b<a, то же неверно ε=(a-b)/2

Дата добавления: 2014-01-14