Теорема Кронекера-Капелли. Правило Крамера. Матричный метод

Лекция 4. Системы линейных уравнений.

Специализированные структуры плазматической мембраны

Плазмолемма многих клеток животных образует выросты различной структуры (микроворсинки, реснички, жгутики). Наиболее часто на поверхности многих животных клеток встречаются микроворсинки. Эти выросты цитоплазмы, ограниченные плазмолеммой, имеющие форму цилиндра с закругленной вершиной. Микроворсинки характерны для клеток эпителиев, но обнаруживаются и у клеток других тканей. Диаметр микроворсинок составляет около 100 нм. Число и длина их различны у разных типов клеток. Значение микроворсинок заключается в значительном увеличении площади клеточной поверхности. Это особенно важно для клеток, участвующих во всасывании. Так, в кишечном эпителии на 1 мм² поверхности насчитывается до 2х10⁸ микроворсинок.

На данном занятии будут рассмотрены такие важные понятия:

ü Системы линейных уравнений.

ü Теорема Кронекера-Капелли.

ü Правило Крамера.

ü Матричный метод.

Определение. Системой линейных уравнений, содержащей 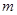уравнений и 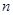неизвестных, называется система вида:

где числа 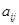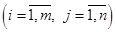называются коэффициентами системы, числа 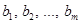называются свободными членами системы, числа называются неизвестными системы и подлежат нахождению.

Определение. Решением системы называется такой набор 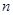значений неизвестных 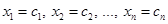, при подстановке которого в систему все уравнения ее обращаются в верные равенства.

Всякое решение системы можно записать в виде матрицы-столбца .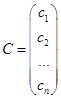

Определение.

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Система уравнений называется несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение.

Совместная система называется неопределенной, если она имеет более одного решения.

Если система совместна, то каждое ее решение называется частным решением системы, а совокупность всех частных решений называется общим решением системы.

Решить систему – это значит выяснить, совместна она или несовместна, и если система совместна, то найти ее общее решение.

Определение. Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение, другими словами, две системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Определение. Система линейных уравнений называется квадратной, если число ее уравнений равно числу ее неизвестных, т.е. :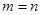

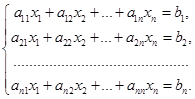
Определение. Система линейных уравнений называется однородной, если все ее свободные члены равны нулю:

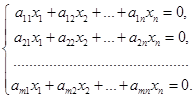
Систему линейных уравнений можно записать в компактной матричной форме:

,

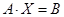где 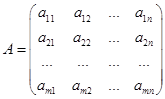- матрица коэффициентов системы, называемая основной матрицей системы,

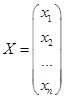- вектор-столбец неизвестных системы,

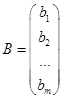- вектор-столбец свободных членов системы.

Заметим, что произведение 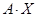определено.

Матрица 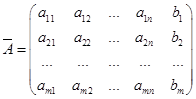называется расширенной матрицей системы.
Теорема Кронекера-Капелли.

Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу расширенной матрицы системы, т.е. .

Например, совместна ли система ?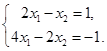

Решение: 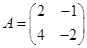. Так как 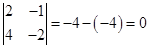и , то .

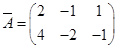. Так как и нет миноров третьего порядка, то .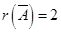

Таким образом, , значит, по теореме Кронекера-Капелли, исходная система несовместна.

Исследовать систему линейных уравнений – это значит выяснить, совместна она или нет, и если совместна, то выяснить, определена она или нет.

Исследование системы линейных уравнений основано на следующих правилах:

1. Если , то система несовместна.

2. Если , то система совместна.

3. Если 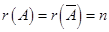, то система совместна и определена.

4. Если 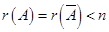, то система совместна и неопределена, и имеет бесчисленное множество решений.

Дата добавления: 2014-01-14