Математическая модель функционирования изделия или системы, используемая при оптимизации их параметров

КРИТЕРИИ И ПОКАЗАТЕЛИ КАЧЕСТВА ТЕХНИЧЕСКИХ СИСТЕМ И ИЗДЕЛИЙ

Статистические или корреляционные зависимости.Статистическая зависимость признаков – это такая зависимость, когда одному и тому же значению одного признака могут соответствовать различные значения другого. Это происходит в силу того, что при статистической зависимости связь устанавливается между признаками (двумя, тремя и т. д.), которые изменяются не только в силу взаимодействия между собой, но и под воздействием множества различных неучтенных факторов. В результате множественного воздействия взаимно переплетающихся факторов связь между признаками существует и проявляется только в тенденции, «в среднем». Поэтому здесь установить наличие взаимосвязи и определить ее количественную меру можно не на основе единичных наблюдений, а лишь применительно к определенной совокупности объектов, т.е. в среднем по отношению к тем или иным массовымобъектам или явлениям. Характеризующие эти объекты количественные показатели в источниковедении и в статистике называются массовыми данными.

Корреляция качественных признаков

Корреляция количественных признаков

Статистические или корреляционные зависимости

Задачи анализа статистических связей. Анализ статистической, или корреляционной, связи предполагает выявление формы связи, а также оценку тесноты связи. Первая задача решается методами регрессионного анализа, вторая — методами корреляционного анализа. Регрессионный анализ сводится к описанию статистической связи с помощью подходящей функциональной зависимости. Корреляционный анализ позволяет оценивать тесноту связи посредством специальных показателей, причем выбор их зависит от вида функциональной зависимости, пригодной для адекватного описания рассматриваемой статистической взаимосвязи.

Один из важных вопросов, возникающих в изучении связей,— установление «направления» зависимости. Пусть для простоты рассматривается связь между двумя признаками у и х. Какой из этих признаков следует считать подверженным влиянию, или результативным (зависимой переменной), какой — оказывающим влияние, или факторным (независимой переменной)?

Первостепенное значение в решении этого вопроса имеет содержательный анализ. Положим, мы рассматриваем связь между производительностью труда рабочих и стажем их работы. По-видимому, результативным признаком следует признать производительность труда, а факторным — стаж рабочего. Не всегда «направление» связи проявляется столь очевидно. Тогда при решении вопроса о выборе результативного признака на первый план выступает постановка содержательной проблемы, для исследования которой используется изучение взаимосвязей. Например, устанавливая «направление» связи между такими признаками, как доходность предприятий и их энерговооруженность, мы должны исходить из того, что же мы хотим установить в действительности: влияние внедрения новой техники и технологии на доходность предприятий или же потенциальные возможности предприятий в овладении передовой техникой и технологией. В первом случае результативным признаком естественно считать доходность, во втором — энерговооруженность.

2. Корреляция количественных признаков. Одной из основных мер связи в корреляционном анализе количественных признаков является линейный коэффициент корреляции.

Парный линейный коэффициент корреляции. С помощью парного линейного коэффициента корреляции измеряется теснота связи между двумя признаками. Линейный коэффициент корреляции чаще всего рассчитывается по формуле

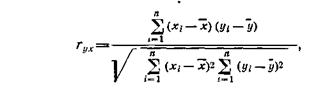где х_iи y_i— значения признаков х и у соответственно для i-ro объекта, i— 1,..., п; п — число объектов; х и у — средние арифметические значения признаков х и у соответственно. Линейный коэффициент корреляции изменяется в пределах от —1 до +1. Равенство коэффициента нулю свидетельствует об отсутствии линейной связи. Равенство коэффициента — 1 или +1 показывает наличие функциональной связи. Знак «+» указывает на связь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «—» — на связь обратную (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).

Как оценить полученное значение коэффициента корреляции? Велико оно или мало? О наличии или об отсутствии связи свидетельствует? Для ответа на эти вопросы проводят проверку значимости коэффициента.

Проверка значимости парного линейного коэффициента корреляции. Коэффициенты корреляции, как правило, рассчитываются для выборочных данных. Чтобы распространить полученные частные результаты на генеральную совокупность, приходится допустить некоторую ошибку, которую можно оценить с помощью средней квадратической ошибки. Средняя квадратическая ошибка для парного линейного коэффициента корреляции достаточно большой выборки вычисляется по формуле , где r— коэффициент корреляции генеральной совокупности; п — объем выборки. Коэффициентом корреляции называют отношение корреляционного момента m_ху к произведению средних квадратичных отклонений r=m_ху/(s_хs_у), корреляционный момент соответственно равен

В математической статистике доказано, что если признаки х и у распределены по нормальному закону, то в достаточно больших выборках коэффициенты корреляции можно считать распределенными нормально со средним значением р и средним квадратическим отклонением s_r. Этот факт используется для построения доверительных интервалов коэффициента корреляции в генеральной совокупности, а также для проверки значимости выборочных коэффициентов корреляции, т.е. для проверки того, могло ли данное значение r получиться в выборке из некоррелированной генеральной совокупности (р = 0) в силу простой случайности.

Очевидно, чем больше отклонение r от р, тем менее вероятно, что оно случайно. Так, для нормального распределения вероятность того, что выборочное значение r отличается от р больше чем на 3s_r, меньше 0,01, т.е. величина нормированного отклонения может превысить значение 3 лишь в одном случае из ста. Таким образом, для проверки значимости r, задаваясь значением вероятности Р (например, Р=0,99), находят по таблицам приложения критическую точку нормированного отклонения и сравнивают ее с фактическим нормированным отклонением, считая что коэффициент корреляции равен 0: . Если критическое нормированное отклонение меньше фактического, то коэффициент корреляции считается значимым, если больше – незначимым.

Основная задача проектировщика-конструктора – это создание технической системы или изделия, наиболее полно отвечающего своему предназначению (потребностям общества), дающего наибольший экономический эффект и обладающего наиболее высокими технико-экономическими и эксплуатационными показателями. Эти показатели еще называют показателями качества изделия или системы.

Показатель качества технического изделия (или системы) – это число, величина которого определяет то или иное свойство (характеристику) изделия (или системы).

В качестве показателей качества системы или изделия, например, могут выступать:

потребляемая мощность или энергоемкость машины;

производительность станка;

экономичность;

прочность конструкции;

надежность функционирования;

вес, металлоемкость конструкции;

габариты конструкции;

объем и стоимость ремонтных работ;

расходы на рабочую силу при создании и эксплуатации системы или изделия;

ресурс долговечности изделия;

моральный ресурс изделия;

межремонтные сроки;

степень автоматизации изделия;

простота и безопасность обслуживания;

удобство разборки и сборки;

удобство управления изделием;

и др.

Набор этих показателей качества зависит от назначения системы или технического изделия, то есть от целей и задач, которые выполняют та или иная система или изделие.

Определение рациональных показателей качества проектируемого изделия или системы и является одной из ключевых задач проектировщика-конструктора. Всякий определенный выбор тех или иных, зависящих от проектировщика, параметров качества изделия (или системы) называется решением задачи обоснования этих показателей. Решения могут быть удачными и неудачными, разумными и неразумными. Рациональными решениями называются такие решения, которые по тем или иным соображениям являются предпочтительнее других.

При проектировании изделия (или системы) проектировщики всегда стремятся сделать его наиболее эффективным в эксплуатации.

Под эффективностью системы или изделия понимают степень пригодности или приспособленности их для использования по назначению.

Величину эффективности определяют как показатели качества (параметры) изделия или системы, так и условия их эксплуатации.

Таким образом, эффективность применения изделия (или системы) является обобщенным показателем качества изделия (или системы), определяющим степень его (ее) пригодности к использованию по назначению.

К условиям эксплуатации изделия (или системы) прежде всего, относятся режим работы, а также условия взаимодействия его с другими изделиями (или техническими системами) и степени достоверности сведений об их характеристиках. К условиям эксплуатации изделия необходимо отнести также климатические и метеорологические условия, в которых работает данное изделие, а также возможности противодействия нормальному его функционированию со стороны других систем или изделий (например, систем, созданных противником).

Оценивать эффективность изделия (системы) необходимо на основе изучения его основных свойств (качества) и условий эксплуатации (применения). Однако ввиду сложности подобной задачи ее иногда декомпозируют (расчленяют) на две самостоятельные задачи. При определении качества (конструктивно-технических параметров) изделия условия боевого применения считаются фиксированными. Затем решается задача по оценке эффективности выбранной конструктивно-технической схемы изделия в различных условиях применения. В результате решения последней задачи выявляются оптимальные способы применения в различных условиях, а также обнаруживаются недостатки изделия, которые можно устранить, изменив некоторые его параметры.

Часть технико-экономических характеристик (показателей качества) изделия (или системы) носят детерминированный характер, другая часть показателей изделия являются случайными величинами.

Например, надежность эксплуатации являются случайными характеристиками качества изделия (системы), то есть ее можно выразить вероятностью того, что изделие сохранит свои основные свойства в любых условиях эксплуатации.

Условия применения (эксплуатации) также необходимо оценивать количественными характеристиками или параметрами, хотя это сделать значительно труднее, чем рационально выбрать параметры качества изделия. Кроме того, следует учитывать, что условия эксплуатации оказывают комплексное влияние на параметры изделия или системы в целом. Например, эффективность применения оружия зависит от характера противодействий противника.

Экономичность изделия (системы) характеризуется затратами на разработку проекта, производство и эксплуатацию всех его элементов.

Решения о выборе тех или иных показателей изделия (или системы) могут быть приняты интуитивно на основе опыта проектировщика (или группы проектировщиков). В этом случае проектировщика можно рассматривать как «черный ящик» (см. предыдущую лекцию).

Обоснованные же решения по выбору тех или иных показателей качества изделия или системы осуществляются на основе оценок эффективности применения изделия в заданных условиях эксплуатации с использованием, так называемого, критерия эффективности.

Критерии эффективности это обычно числовые характеристики, отражающие степень соответствия изделия своему назначению при определенных условиях применения. Критерий эффективности должен отражать назначение системы или изделия. Как числовая характеристика он должен являться функцией параметров, характеризующих свойства (качество) изделия и условий его применения. Поэтому критерий эффективности чаще всего еще называются целевой функцией оптимизации изделия (или целевым функционалом системы). Критерий отличается от показателя изделия тем, что в нем фигурирует не число, а функция от параметров изделия и указано правило, по которому определяют оптимальные значения этих параметров.

Критерий (целевая функция) технической системы или изделия – это правило, по которому определяются оптимальные конструктивно-технические и эксплутационные характеристики системы или изделия.

Выбор критерия оптимизации изделия или системы является не простой задачей.

Чем больше параметров изделия входит в критерий, тем он полнее. Однако при выборе функциональной связи критерия эффективности с параметрами качества и условиями применения системы или изделия необходимо учитывать не одинаковую значимость отдельных свойств и условий применения. В качестве критериев целесообразно выбирать величины, имеющие определенный физический смысл.

В связи с разнообразием задач, которые решаются различными системами или изделиями, установить единый, универсальный критерий эффективности нельзя. При выборе критерия для изделия (или системы) следует учитывать его специфические особенности.

В принципе любая технико-экономическая характеристика (показатель качества) изделия или системы может быть принята в качестве целевой функции.

Так, например, в качестве критерия для оптимизации параметров изделий машиностроительного производства могут быть выбраны следующие:

коэффициент полезного действия;

производительность;

экономичность;

прочность;

надежность;

вес;

металлоемкость;

габариты;

энергоемкость;

объем и стоимость ремонтных работ;

расходы на рабочую силу;

ресурс долговечности;

межремонтные сроки;

моральный ресурс;

и др.

Удельный вес каждого из перечисленных критериев зависит от назначения машины:

в машинах-генераторах и преобразователях энергии на первом плане стоит величина к.п.д., определяющего совершенство преобразования затрачиваемой энергии в полезную;

в машинах-орудиях — производительность, четкость и безотказность действия;

в металлорежущих станках — производительность, точность обработки, диапазон выполняемых операций;

в приборостроении — чувствительность, точность; стабильность показаний;

в транспортной технике, особенно в авиационной и ракетной, - малый вес конструкции, высокий к.п.д. двигателя, обуславливающий малый вес бортового запаса топлива.

Будем в дальнейшем обозначать показатель эффективности буквой W.

Конкретный вид показателя эффективности W,. которым следует пользоваться при численной оценке эффективности, зависит от специфики основного назначения рассматриваемого изделия, его целевой направленности, а так же от задачи проектирования (исследования), которая может быть поставлена в той или другой форме.

Применение изделий сопровождается большим числом случайных факторов, которые определяются случайными ошибками работы системы или изделия, разбросом конструктивных параметров изделия и условий его применения. Поэтому в этом случае результаты функционирования изделия должны рассматриваться как функции случайных величин, а критерии эффективности обычно представляют собой вероятностные характеристики. В этом случае в качестве критерия чаще всего используются вероятности различных событий и математические ожидания — случайных величин. То есть, многие функции изделия или системы выполняются в условиях, содержащих элемент случайности, например, изделие, предназначенное для применения в военных операциях. В этих случаях результат функционирования изделия в военной операции, даже организованной строго определенным образом, не может быть точно предсказан, остается случайным. Если это так, то в качестве показателя эффективности W выбирается не просто характеристика исхода операции, а ее среднее значение (математическое ожидание).

Или, например, если мы хотим после создания изделия получить максимальную прибыль, то так как прибыль величина случайная, то в качестве критерия эффективности берется средняя прибыль. В других случаях, когда целью будущего изделия или системы является осуществление случайного события (например, для создаваемых артиллерийских орудий таким событием является поражение группы целей, которое является конечно случайным) в качестве показателя эффективности берут вероятность этого события. (например, вероятность того, что в результате артиллерийского залпа группа целей будет поражена).

Правильный выбор показателей эффективности — необходимое условие полезности исследований, применяемых при обосновании параметров (показателей качества) изделия или систем при проектировании. Рассмотрим ряд примеров, в каждом из которых показатель эффективности W выбран в соответствии с целевой направленностью проектируемого изделия или технической системы.

Примеры определения целевой функции (критерия) оптимизации конструктивных параметров изделия.

Пример 1. Разрабатывается машиностроительный сборочный цех, причем производство в этом цеху должно приносить прибыль заводу, т.е. быть рентабельным. Критерий эффективности — максимальная прибыль (или средняя прибыль), приносимая цехом за хозяйственный год.

Пример 2 Создается истребитель. Целью будущей операции — сбить самолет заданной группой создаваемых истребителей. Критерием эффективности (целевой функции) является максимум вероятности поражения самолета.

Пример 3. Ремонтная мастерская занимается обслуживанием машин; ее рентабельность определяется количеством машин, обслуженных в течение дня. Для нее разрабатывается новый станок или машина для увеличения числа обслуженных машин. Критерий эффективности — среднее число машин, обслуженных за день («среднее» потому, что фактическое число случайно).

Пример 4. Разрабатывается мобильная группа радиолокационных станций. Эта группа радиолокационных станций в определенном районе будет вести наблюдение за воздушным пространством в своей зоне ответственности. Задача группы — обнаружить любой самолет, если он появится в их зоне ответственности. Критерий эффективности — максимум вероятности обнаружения любого самолета, появившегося в районе.

Пример 5. Предпринимается ряд мер по повышению надежности электронной цифровой вычислительной машины. Цель модернизации ЭВМ — уменьшить частоту появления ее неисправностей («сбоев»), или; что равносильно, увеличить средний промежуток времени между сбоями («наработку на отказ»). Проще говоря, требуется повысить надежность работы ЭВМ. Критерий эффективности — максимум среднего времени безотказной работы ЭВМ (или среднее относительное время исправной работы).

Во всех рассмотренных примерах показатель эффективности, каков бы он ни был, требовалось обратить в максимум («чем больше, тем лучше»). Вообще, это не обязательно: при проектировании часто пользуются показателями, которые требуется обратить не в максимум, а в минимум («чем меньше, тем лучше»).

Например, в примере 4 можно было бы в качестве критерия эффективности взять «минимум вероятность того, что появившийся самолет не будет обнаружен» — этот показатель желательно сделать как можно меньше. В примере 5 за критерий эффективности можно было бы принять «минимум среднего числа сбоев за сутки».

Пример 6. Если оценивается какая-то проектируемая система, обеспечивающая наведение снаряда на цель, то в качестве критерия эффективности можно выбрать среднее значение «промаха» снаряда (расстояния от траектории до центра цели), которое желательно сделать как можно меньше.

Пример 7. Создается машина для уборки улиц от снега. Желательно сделать продуктивность такой машины такой, чтобы количество машин (наряд машин), выделяемых на уборку снега с улиц города было минимальным. Стоимость такой системы машин желательно, чтобы тоже была минимальной.

Таким образом, во многих задачах проектных исследований разумное решение должно обеспечивать не максимум, а минимум некоторого показателя.

Очевидно, что случай, когда критерий эффективности W надо обратить в максимум, легко сводится к задаче минимизации (для этого достаточно, например, изменить знак величины W). Поэтому в дальнейшем, рассматривая в общем виде задачу исследования операций, мы будем для простоты говорить только о случае, когда W требуется обратить в минимум. Что касается практических конкретных задач, то мы будем пользоваться как показателями эффективности, которые требуется максимизировать, так и теми, которые требуется минимизировать.

Для применения количественных методов исследования при проектировании всегда требуется построить ту или другую математическую модель функционирования изделия или системы. При построении математической модели функционирования изделия каким-то образом реальные процессы функционирования упрощаются, схематизируются; из бесчисленного множества факторов, влияющих на функционирование изделия, выделяется сравнительно небольшое количество важнейших, и полученная схема описывается с помощью того или другого математического аппарата. В результате устанавливаются количественные связи между условиями функционирования, параметрами изделия (системы) и критерием эффективности (или критериями, если их несколько).

Чем удачнее подобрана математическая модель, тем лучше она отражает характерные черты функционирования проектируемого изделия или системы, тем успешнее и полезнее будет проведено исследование и вытекающие из него рекомендации по требуемым параметрам будущего изделия (показателям качества)

Общих способов построения математических моделей не существует. В каждом конкретном случае модель строится, исходя из целевой направленности изделия и задач научного исследования, с учетом требуемой точности решения, а также точности, с какой могут быть известны исходные данные.

Требования к модели противоречивы. С одной стороны, она должна быть достаточно полной, т. е. в ней должны быть учтены все важные факторы, от которых существенно зависят проектные параметры нового изделия. С другой стороны, модель должна быть достаточно простой для того, чтобы можно было установить обозримые (желательно — аналитические) зависимости между входящими в нее параметрами. Модель не должна быть «засорена» множеством мелких, второстепенных факторов — их учет усложняет математический анализ и делает результаты исследования трудно обозримыми.

Одним словом, искусство составлять математические модели есть именно искусство, и опыт в этом деле приобретается постепенно. Две опасности всегда подстерегают составителя модели: первая — утонуть в подробностях («из-за деревьев не увидеть леса»); вторая— слишком огрубить явление («выплеснуть из ванны вместе с водой и ребенка». В сложных случаях, когда построение модели вызывает наибольшее сомнение, полезным оказывается своеобразный «спор моделей», когда одно и то же явление исследуется на нескольких моделях. Если научные выводы и рекомендации от модели к модели меняются мало, то — серьезный аргумент в пользу объективности проектного исследования. Характерным для сложных задач исследования функционирования изделий и систем является также повторное обращение к модели после того, как первый цикл исследований выполнен, возвращаются снова к модели и вносят в нее необходимые коррективы.

Построение математической модели — наиболее важная и ответственная часть проектного исследования, требующая глубоких знаний не только и не столько в математике, сколько в существе моделируемых явлений. Однако раз созданная удачная модель может найти применение и далеко за пределами того круга явлений, для которого она первоначально создавалась. Так, например, математические модели массового обслуживания нашли широкое применение в целом ряде областей, далеких, с первого взгляда, от массового обслуживания (надежность технических устройств, организация автоматизированного производства, задачи ПВО и др.). Математические модели, первоначально предназначенные для описания динамики развития биологических популяций, находят широкое применение при описании боевых действий и наоборот — боевые модели с успехом применяются в биологии.

Математические модели, применяемые в настоящее время при проектировании изделий, можно грубо подразделить на два класса: аналитические и статистические.

Для первых характерно установление формульных, аналитических зависимостей между параметрами задачи, записанных в любом виде: алгебраические уравнения, обыкновенные дифференциальные уравнения, уравнения с частными производными и т. д. Чтобы такое аналитическое описание операции было возможно, как правило, нужно принять те или иные допущения или упрощения. С помощью аналитических моделей удается с удовлетворительной точностью описать только сравнительно простое функционирование изделий и систем, где число взаимодействующих элементов не слишком велико. В операциях же большого масштаба, сложных, в которых переплетается действие огромного количества факторов в том числе и случайных, на первый план выходит метод статистического моделирования. Он состоит в том, что процесс функционирования изделия как бы «копируется» на вычислительной машине, со всеми сопровождающими его случайностями. Всякий раз, когда в ход операции вмешивается какой-либо случайный фактор, его влияние учитывается посредством «розыгрыша», напоминающего бросание жребия. В результате многократного повторения такой процедуры удается получить интересующие нас характеристики исхода с любой степенью точности.

Статистические модели имеют перед аналитическими то преимущество, что они позволяют учесть большее число факторов и не требуют грубых упрощений и допущений. Зато результаты статистического моделирования труднее поддаются анализу и осмыслению. Более грубые аналитические модели описывают явление лишь приближенно, зато результаты более наглядны и отчетливее отражают присущие функционированию изделия основные закономерности. Наилучшие результаты получаются при совместном применении аналитических и статистических моделей: простая аналитическая модель позволяет вчерне разобраться в основных закономерностях явления, наметить главные его контуры, а любое дальнейшее уточнение может быть получено статистическим моделированием.

При создании математических моделей функционирования изделий и систем используются методы следующих наук: физики, теоретической механики, математики, теории вероятностей, исследования операций, логики, теории игр, теории принятия решений, сопротивления материалов, теории машин и механизмов и др.

Дата добавления: 2014-01-14