Статистическая проверка гипотез

Статистические или корреляционные зависимости.Статистическая зависимость признаков – это такая зависимость, когда одному и тому же значению одного признака могут соответствовать различные значения другого. Это происходит в силу того, что при статистической зависимости связь устанавливается между признаками (двумя, тремя и т. д.), которые изменяются не только в силу взаимодействия между собой, но и под воздействием множества различных неучтенных факторов. В результате множественного воздействия взаимно переплетающихся факторов связь между признаками существует и проявляется только в тенденции, «в среднем». Поэтому здесь установить наличие взаимосвязи и определить ее количественную меру можно не на основе единичных наблюдений, а лишь применительно к определенной совокупности объектов, т.е. в среднем по отношению к тем или иным массовымобъектам или явлениям. Характеризующие эти объекты количественные показатели в источниковедении и в статистике называются массовыми данными.

Корреляция качественных признаков

Корреляция количественных признаков

Статистические или корреляционные зависимости

Задачи анализа статистических связей. Анализ статистической, или корреляционной, связи предполагает выявление формы связи, а также оценку тесноты связи. Первая задача решается методами регрессионного анализа, вторая — методами корреляционного анализа. Регрессионный анализ сводится к описанию статистической связи с помощью подходящей функциональной зависимости. Корреляционный анализ позволяет оценивать тесноту связи посредством специальных показателей, причем выбор их зависит от вида функциональной зависимости, пригодной для адекватного описания рассматриваемой статистической взаимосвязи.

Один из важных вопросов, возникающих в изучении связей,— установление «направления» зависимости. Пусть для простоты рассматривается связь между двумя признаками у и х. Какой из этих признаков следует считать подверженным влиянию, или результативным (зависимой переменной), какой — оказывающим влияние, или факторным (независимой переменной)?

Первостепенное значение в решении этого вопроса имеет содержательный анализ. Положим, мы рассматриваем связь между производительностью труда рабочих и стажем их работы. По-видимому, результативным признаком следует признать производительность труда, а факторным — стаж рабочего. Не всегда «направление» связи проявляется столь очевидно. Тогда при решении вопроса о выборе результативного признака на первый план выступает постановка содержательной проблемы, для исследования которой используется изучение взаимосвязей. Например, устанавливая «направление» связи между такими признаками, как доходность предприятий и их энерговооруженность, мы должны исходить из того, что же мы хотим установить в действительности: влияние внедрения новой техники и технологии на доходность предприятий или же потенциальные возможности предприятий в овладении передовой техникой и технологией. В первом случае результативным признаком естественно считать доходность, во втором — энерговооруженность.

2. Корреляция количественных признаков. Одной из основных мер связи в корреляционном анализе количественных признаков является линейный коэффициент корреляции.

Парный линейный коэффициент корреляции. С помощью парного линейного коэффициента корреляции измеряется теснота связи между двумя признаками. Линейный коэффициент корреляции чаще всего рассчитывается по формуле

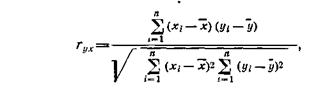где х_iи y_i— значения признаков х и у соответственно для i-ro объекта, i— 1,..., п; п — число объектов; х и у — средние арифметические значения признаков х и у соответственно. Линейный коэффициент корреляции изменяется в пределах от —1 до +1. Равенство коэффициента нулю свидетельствует об отсутствии линейной связи. Равенство коэффициента — 1 или +1 показывает наличие функциональной связи. Знак «+» указывает на связь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «—» — на связь обратную (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).

Как оценить полученное значение коэффициента корреляции? Велико оно или мало? О наличии или об отсутствии связи свидетельствует? Для ответа на эти вопросы проводят проверку значимости коэффициента.

Проверка значимости парного линейного коэффициента корреляции. Коэффициенты корреляции, как правило, рассчитываются для выборочных данных. Чтобы распространить полученные частные результаты на генеральную совокупность, приходится допустить некоторую ошибку, которую можно оценить с помощью средней квадратической ошибки. Средняя квадратическая ошибка для парного линейного коэффициента корреляции достаточно большой выборки вычисляется по формуле 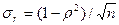, где r— коэффициент корреляции генеральной совокупности; п — объем выборки. Коэффициентом корреляции называют отношение корреляционного момента m_ху к произведению средних квадратичных отклонений r=m_ху/(s_хs_у), корреляционный момент соответственно равен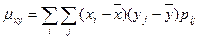

В математической статистике доказано, что если признаки х и у распределены по нормальному закону, то в достаточно больших выборках коэффициенты корреляции можно считать распределенными нормально со средним значением р и средним квадратическим отклонением s_r. Этот факт используется для построения доверительных интервалов коэффициента корреляции в генеральной совокупности, а также для проверки значимости выборочных коэффициентов корреляции, т.е. для проверки того, могло ли данное значение r получиться в выборке из некоррелированной генеральной совокупности (р = 0) в силу простой случайности.

Очевидно, чем больше отклонение r от р, тем менее вероятно, что оно случайно. Так, для нормального распределения вероятность того, что выборочное значение r отличается от р больше чем на 3s_r, меньше 0,01, т.е. величина нормированного отклонения 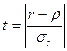может превысить значение 3 лишь в одном случае из ста. Таким образом, для проверки значимости r, задаваясь значением вероятности Р (например, Р=0,99), находят по таблицам приложения критическую точку нормированного отклонения и сравнивают ее с фактическим нормированным отклонением, считая что коэффициент корреляции равен 0: 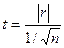. Если критическое нормированное отклонение меньше фактического, то коэффициент корреляции считается значимым, если больше – незначимым.

Дата добавления: 2014-01-14