Функция Грина для задачи Дирихле

Лекция №4

Рассмотрим задачу Дирихле:

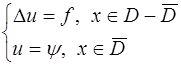, (17)

где D – ограниченная область, а 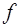и ­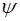 непрерывные функции.

Предположим, что

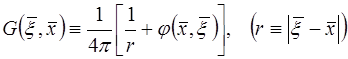(18)

­ фундаментальное решение уравнения Лапласа в области D и обращается в нуль на ее границе 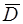. Для этого функция 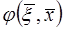должна быть решением граничной задачи:

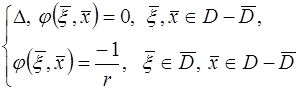(19)

Подставив в формулу

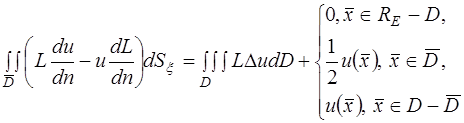(20)

.

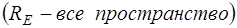Значения величин, заданные в граничной задаче (17), и положив

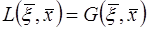, получим

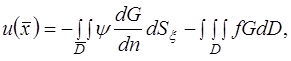
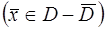, (21)

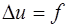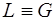так как в(20) и на 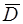обращается в нуль.

Если фундаментальное решение 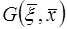и его производная 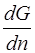существует, то эта формула дает решение задачи Дирихле (17), принадлежащее рассматриваемому классу функций в интегральной форме. Тем самым, решение задачи Дирихле (17) общего вида для неоднородного уравнения может быть заменено разысканием функции 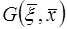, для чего требуется найти решение задачи Дирихле (19) частного вида для однородного уравнения. Фундаментальное решение 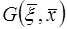называют функцией Грина задачи (17) Дирихле или функцией Грина оператора Лапласа. Полученный результат распространяется и на внешнюю задачу Дирихле для уравнения Лапласа (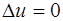). Аналогичные результаты могли быть получены для задачи Неймана и смешанной задачи:

;

.

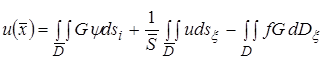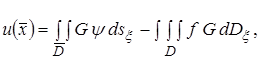
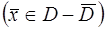Дата добавления: 2014-01-14