Уравнения Лапласа

Метод конформных отображений решения

Функция Грина для задачи Дирихле.

Лекция №4

Функция Грина для задачи Дирихле. (см.лекцию №2)

Метод конформных отображений решения уравнения Лапласа

Имеется задача:

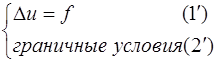
(1-го рода – задача Дирихле; 2-го рода ­ задача Неймана, 3-го рода ­ смешанная задача).

Рассмотрим для простоты задачу Дирихле (1).

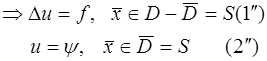
Решение задачи или определяется, во-первых, областью, в которой ищется функция , зависящая от формы области 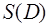; во-вторых, граничными условиями.

Решение задачи для уравнения Пуассона всегда может быть

сведено к решению уравнения Лапласа 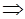(например, функция Грина для задачи Дирихле)

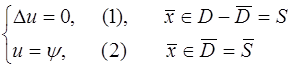
Решение задачи (1)–(2), т.е. уравнение Лапласа известно для канонических областей (круг, квадрат, кольцо, верхняя полуплоскость и т.п.). Для областей сложной геометрической формы непосредственное решение для этой области представляет большие трудности 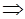. Зная решения уравнения Лапласа для канонических областей и функцию 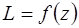, конформно отображающую область 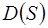на каноническую область, и функцию 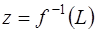, можно определить решение для области произвольной формы

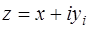; (3)

Причем, выполняется 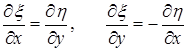, (4)

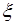т.е. и ­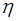 сопряженно-гармонические функции (условия моногенности Коши-Римана). Уравнение Лапласа остается инвариантным относительно преобразований, доставляемых моногенными функциями комплексной переменной.

Преобразования, даваемые функциями (3) будут конформными (бесконечно малые области плоскости переводятся в подобщие им фигуры в плоскости 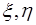, где .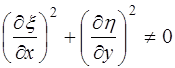

Причем, если область односвязная, то область целесообразно отобразить на круг или верхнюю полуплоскость 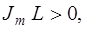и на кольцо, если область двухсвязная. Практически для любой области 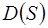можно построить приближенные, конформно отображающие функции. Например, для многоугольных областей можно воспользоваться формулой Кристоффеля-Шварца.

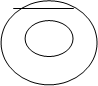
1) Например, функция, конформно отображающая прямоугольник со сторонами 2а и 2 в на верхнюю полуплоскость имеет вид:

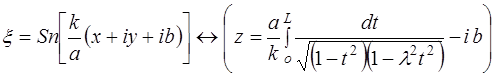, (5)

где ­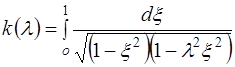 полный эллиптический интеграл 1-го рода, 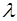- определяется из уравнения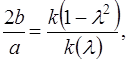 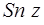- функция Якоби (эллиптический синус)

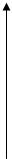
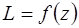
L

y

z

S

x

z=f^-1

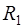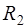
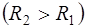2) Функция, отображающая эксцентрически расположенные круглые трубы радиуса и на кольцо имеет вид:

;

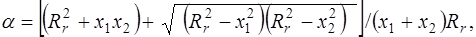
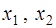- координаты точки пересечения внутренней окружности с осью абсцисс

y

R₂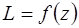

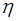
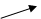
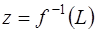
К уравнениям Лапласа и Пуассона приводят многочисленные задачи теории теплопроводности, электростатики, гидродинамики, теории упругости и т.д. Это уравнения эллиптического типа. Обычно различают три основных вида граничных условий и, соответственно, три основных вида граничной задачи:

1) 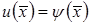, 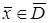- первая граничная задача (задача Дирихле);

2) - вторая граничная задача (задача Неймана); (15)

3) - третья (смешанная) граничная задача.

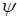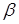Здесь и - непрерывные функции, определенные на 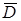; - внешняя нормаль к .

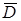Если область, в которой ищется решение уравнения, ограничена, то граничная задача называется внутренней. Если же эта область является частью пространства, лежащей вне некоторой ограниченной области, то граничная задача называется внешней.

Задачу математической физики называют корректно поставленной, если ее решение существует, единственно и непрерывно зависит от данных задачи. Корректная постановка задачи обычно обеспечивает физическую содержательность решения. Существует основная группа условий, обеспечивающая корректность той или иной граничной задачи. Она сводится к следующему. Функция, дающая решение граничной задачи для уравнения в частных производных 2-го порядка должна:

1) быть непрерывна в области, в которой ставится задача, вплоть до границы области;

2) внутри области иметь непрерывные вторые производные и удовлетворять заданному уравнению;

3) на границе области удовлетворять заданному граничному условию;

4) если область трехмерна и бесконечна, то при стремится к нулю.

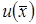Решения граничных задач, поставленных в трехмерных областях, удовлетворяющие перечисленным условиям называют регулярными. Говорят, что в точке функция является гармонической, если в этой точке она имеет непрерывные вторые производные и удовлетворяет уравнению Лапласа. Функция 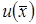является гармонической в замкнутой области D, если она:

1) непрерывна в этой области; 2) гармонична во всех внутренних точках области; 3) если область D бесконечна, то при 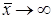вдоль любого луча, стремится к нулю .

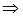2) Регулярные решения граничных задач для уравнения Лапласа являются гармоническими функциями.

Если функция 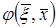в области D гармонична по координатам точки 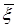и непрерывна вместе со своими первыми производными, то функцию

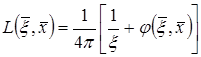(16) называют фундаментальным решением уравнения Лапласа, где

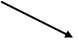
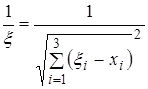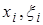, - координаты двух точек,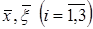

удовлетворяет уравнению Лапласа при .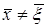

Дата добавления: 2014-01-14