Общие сведения. Потери давления при движении газа

Потери давления при движении газа

Силы, действующие в газе

Общие сведения

Лекцию разработал

Доцент А. Кивокурцев

2.1 Уравнение равновесия газов.

3. Основы теории движения газа

3.1 Основные положения.

4.1 Характер движения газа

4.2Сопротивление трению

4.3 Местные сопротивления

4.3.1 Внезапное расширение.

4.3.2 Поворот потока.

5. Гидравлический расчет наклонных распределительных газопроводов

Все расчеты систем газораспределения осуществляются на ос­нове законов гидравлики (механики газов), которые рассматрива­ют движущиеся среды как среды сплошные, не касаясь вопросов их молекулярного строения. Поэтому нет никакого принципиаль­ного различия между законами, управляющими движением газов и жидкостей. Разделение нетвердых тел на среды сжимаемые (соб­ственно газы) и несжимаемые (собственно жидкости) не совсем точно. Строго говоря, капельные жидкости обладают некоторой способностью сжиматься и, наоборот, газы очень часто можно рассматривать как тела несжимаемые. Законы механики твердого тела непосредственно относятся к механике жидкостей и газов, однако для последних все осложняется способностью отдельных частиц и элементов к взаимному перемещению друг относительно друга. Вследствие этого полное изменение во времени какой-ни­будь величины (например, давления, скорости, температуры и т.д.), характеризующей движущуюся жидкую частицу, слагается из мес­тного (локального) и конвективного изменений и при переходе к бесконечно малым величинам равно их сумме.

Так, например, полная производная давления р, действующего на движущуюся в потоке жидкую частицу, выражается следующим образом:

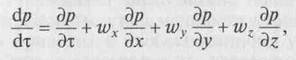
где τ — время; w_х, w_y, w_z — составляющие скорости по координат­ным осям. Выражение получило название субстанциальной производной. Выражение дρ/дτ— местное изменение, а остальные члены правой части уравнения характеризуют конвективное изменение.

Различают установившиеся или стационарные процессы, когда ха­рактеризующие эти процессы величины в каждой точке пространства не зависят от времени, и неустановившиеся или нестационарные про­цессы, когда эти величины зависят от времени. Например, при установившемся движении газа в трубе скорости и давления в каждой точке постоянны, поэтому в уравнении дρ/дτ = 0. Опыт показывает, что если поток газа или жидкости направить вдоль поверхности, то бывшее ранее равномерным поле скоростей изменяется (рис. 1).

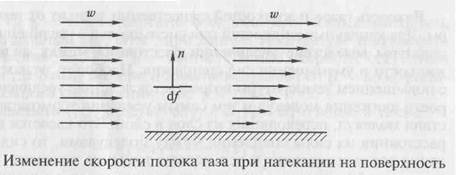
рис1

Полем какой-нибудь физической величины называется распределе­ние значений ее в рассматриваемой области.

Изменение скоростного поля при натекании потока на плас­тинку объясняется тем, что жидкости и газы обладают внутрен­ним трением, или, иначе, вязкостью. Вследствие вязкости поток стенкой затормаживается, при этом скорость потока у поверхно­сти пластинки равна нулю (w = 0), она увеличивается по мере отдаления от пластинки до начального значения. В потоке жидко­сти или газа, направленном вдоль какого-нибудь тела, между сло­ями, движущимися с разной скоростью, возникает сила трения, значение которой может быть найдено из формулы

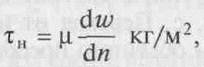
где τ_н — касательное напряжение, т.е. сила трения, отнесенная к
единице поверхности, расположенной вдоль по потоку между сло­ями; μ—коэффициент пропорциональности, кгс/м², называет­ся коэффициентом динамической вязкости;------------------ дω/дn градиент скорости в направлении, нормальном к этой поверхности.

Различают

• коэффициент кинематической вязкости, м²/с,

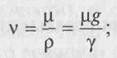
• коэффициент внутреннего трения, кг/(м *с),

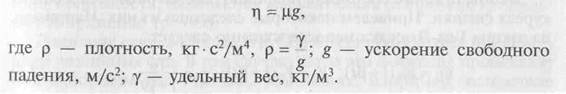
Вязкость газов и жидкостей существенно зависит от температу­ры. Для капельных жидкостей она уменьшается с увеличением тем­пературы вследствие увеличения расстояния между молекулами жидкости и уменьшения сил сцепления. Наоборот, вязкость газов с повышением температуры возрастает вследствие увеличения ско­рости движения молекул и тем самым усиления тормозящего дей­ствия молекул, переходящих из слоя в слой. Что касается влияния расстояния на силы сцепления между молекулами, то силы сцеп­ления для газа невелики и решающего значения не имеют. Зависи­мость коэффициента внутреннего трения газов от температуры определяется по формуле, найденной опытным путем:

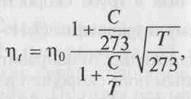
где ηо — значение коэффициента внутреннего трения при 0°С;

С- постоянная величина, различная для разных газов; Т— абсо­лютная температура (Т= t+ 273).

Согласно кинетической теории газов их вязкость не зависит от давления, так как пропорциональна плотности и длине свободного пробега молекул. На практике в ряде случаев пренебрегают вязкими свойствами среды. Среда, не обладающая вязкостью, называется иде­альной. В дальнейшем будем называть газом текущую среду в широком смысле слова, характеризуя ее особенности только терминами, име­ющими общее значение: сжимаемая, несжимаемая, идеальная, ре­альная. Используем следующую систему единиц: метр, килограмм (силы), секунда — м, кг, с. Переход от одной системы единиц к другой совершается путем обычного преобразования, например:

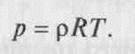
Законы газового состояния подробно рассматриваются в общих курсах физики. Приведем некоторые следствия из них. Например, из закона Гей-Люссака непосредственно следует:

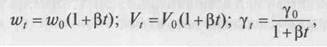
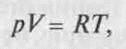
которое дает зависимость произведения р У от температуры. В урав­нении R — газовая постоянная, из этого уравнения следует, что для конкретного газа

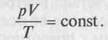
На основе выражения получены зависимости:

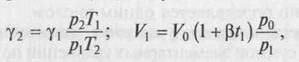
где у₁, у₂ — удельный вес газа соответственно при температурах Т₁, Т₂ и давлениях р₁,р_г ; V_o — объем газа при нормальных условиях; р₀ — атмосферное давление, выраженное в тех же единицах, что и р₁ р₂

Дата добавления: 2014-01-14