Основы теории движения газа

Основные положения. Поведение потока газа или жидкости можно описать двумя способами. Первый из них (способ Лагранжа) заключается в том, что указывается поведение с течением времени каждой частицы, составляющей поток: изменение поло­жения ее траектории, изменение по времени действующих на каж­дую частицу давлений, изменение температуры частиц и т.д. При этом способе описания потока дается история поведения характе­ристик каждой частицы, составляющей поток.

Второй способ (способ Эйлера) заключается в том, что указывается, что происходит в каждой точке изучаемого потока в каж­дый данный момент в результате прохождения через эти точки различных частиц движущейся среды, каковы скорости в каждой точке изучаемого потока, давления, температуры и т. п. Таким об­разом, этот способ дает как бы моментальные снимки состояния потока во всех его точках.

При описании движения среды по первому способу использу­ется понятие траектории — пути, по которому движется частица. Во втором способе используется понятие линии тока — линии, касательные к которой в каждой точке совпадают с направлением скорости потока в данной точке. При установившемся течении, когда скорости в каждой точке потока не изменяются со време­нем, линии тока и траектории совпадают.

Проведем через замкнутую кривую (например, в плоскости, перпендикулярной к направлению потока) линии тока, тогда мы получим так называемую трубку тока, содержимое трубки тока называется жидкой нитью. Трубка тока обладает следующим свой­ством: расход через любое ее сечение одинаков, так как скорости касательны к линиям тока и через стенки трубки жидкость не бу­дет ни втекать, ни вытекать.

В основу теории движения газа положены следующие уравне­ния: неразрывность течения (сплошность); движение идеальной жидкости; движение вязкого газа; уравнение Бернулли; уравнение импульсов Эйлера.

Уравнение неразрывности представляет собой резуль­тат применения закона сохранения массы к несжимаемой движу­щейся среде (газу или жидкости):

для одномерного движения вдоль оси X: дw_х/дх=0

Для течения сжимаемого газа уравнение имеет вид

Уравнения неразрывности получают значительно более простой вид для трубки тока в условиях установившегося (стационарного) потока. Количество газа, м³/с, проходящего через одно из сечений трубки тока, - G₁ =w ₁ f₁y₁, через другое сечение — G₂ = w₂f₂y₂, где w ₁и w ₂ — скорости газа в этих сечениях, м/с; f₁ и f ₂ — площади сечений, м²; γ₁и γ₂ — удельный вес газа в сечениях, кг/м³.

Так как через боковые поверхности трубки тока ни расхода, ни прихода газа нет, то при установившемся течении приход газа че­рез одно сечение должен быть равен расходу газа через другое се­чение:

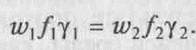
Это и есть уравнение неразрывности в рассматриваемом случае.

Если удельный вес газа при движении не изменяется, т.е. γ₁₌γ₂, то уравнение неразрывности принимает вид w ₁ f₁=w₂f₂.

Эти уравнения действительны для течения в трубах или кана­лах, если за w принимать среднюю скорость по сечению, опреде­ляемую как w = V/f, где V— секундный объем газа или жидкости, протекающих через сечение. В таком виде уравнения неразрывнос­ти широко применяются в инженерных расчетах.

Уравнение движения идеального газа выводится с учетом силы тяжести, давления и инерции (силы вязкости от­сутствуют) и для трехмерного потока оно имеет вид:

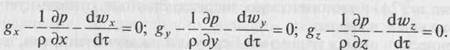
Размерность каждого члена этих уравнений — м/с².

Уравнение движения вязкого газа — в этом случае кроме рассмотренных ранее сил в жидкости будут действовать так­же силы вязкости. Действие вязкости на поток жидкости в трубах или каналах проявляется в том, что скорости по сечению потока будут неодинаковы. В середине потока скорости имеют максималь­ные значения и уменьшаются к стенкам. Непосредственно у самой стенки скорости равны нулю. С учетом сжимаемости газа одномер­ное уравнение движения вязкого газа:

Уравнение неразрывности (сплошности) и уравнение движения газа — два основных уравнения механики газов. Система, состоящая из двух дифференциальных уравнений, имеет мно­жество решений в соответствии с бесчисленным количеством част­ных случаев течения газа или жидкости. Для однозначного решения этой системы необходимо присоединение дополнительных уравне­ний, описывающих так называемые краевые условия. С помощью этих дополнительных уравнений из всей совокупности явлений дви­жения газа выделяется данный конкретный случай. Решение такой системы уравнений — задача математически очень сложная. До сих пор точное решение удалось получить только для небольшого числа простейших случаев. Однако понимание задач механики газов и уме­ние находить их приближенные важные для инженерной практики решения невозможны без изучения основных дифференциальных уравнений механики газов. Далее дается решение уравнения Эйлера для трубки тока и решение задачи одномерного ламинарного тече­ния вязкой жидкости в круглой трубе и указаны области примене­ния полученных выводов для практических задач.

Уравнение Бернулли для одномерного пространства имеет вид

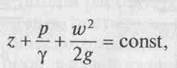
где z — геометрическая высота, выражает удельную энергию по­ложения частицы, т.е. энергию, отнесенную к 1 кг движущейся жидкости (или газа), м; р/γ — пьезометрическая высота, выражает удельную энергию давления, м; w²/2g — скоростная высота, вы­ражает удельную кинетическую энергию, м.

Уравнение представляет собой закон сохранения энер­гии, поскольку сумма (z + p/γ) характеризует потенциальную, а от­ношение w²/2g — кинетическую энергию струйки, отнесенную к 1 кг движущейся среды.

Физический смысл уравнения Бернулли заключается в том, что при установившемся движении частицы идеальной несжимаемой жидкости вдоль линии тока сумма геометрической, пьезометриче­ской и скоростной высот не изменяется.

Если отнести энергию движущейся частицы не к 1 кг, а к 1 м³ движущейся жидкости, то уравнение Бернулли примет вид

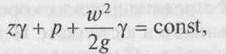
где zγ - геометрический напор, м*кг/м³ = кг/м² (мм вод. ст., Па); р _ пьезометрический (статический) напор, кг/м² (мм вод. ст., Па); w²y/2g — скоростной (динамический) напор, кг/м² (мм вод. ст., Па).

В практических инженерных задачах пользуются средним значе­нием скорости по сечению потока, определяя ее как отношение секундного расхода газа к площади сечения потока: w_cp = V/f.

Действительная скорость в различных точках сечения отличает­ся от этото значения на некоторую величину Aw, различную для разных точек по абсолютному значению и по знаку, поэтому урав­нение для потока в целом при плавно изменяющемся сечении бу­дет иметь следующий вид:

Коэффициент α зависит от неравномерности распределения ско­ростей по сечению

Профиль скорости потока газа в трубопроводе при ламинарном (а) и при турбулентном (б) режимах протекания газа

Для ламинарного потока в круглой трубе, где распределение скоростей по сечению потока соответствует параболе, а = 2. Для установившегося турбулентного течения в трубах а - 1,1... 1,13.

Применяя уравнение Бернулли для расчета движения газов и жидкостей по каналам и трубам с неплавным изменением сече­ния, необходимо выбирать сечения, для которых составляются уравнения, на достаточно большом расстоянии от мест резких расширений и сужений потока или резких изменений его направ­ления.

Уравнение было выведено из предположения, что газ несжима­ем и температура его постоянна.

Уравнение для идеального газа, учитывающее внутреннюю энер­гию газа и предназначенное для расчетов, когда изменяется тем­пература потока, имеет вид

где Е — внутренняя энергия газа при температуре t (считая от 0°С); А— механический эквивалент теплоты, А = 1*10^-3 кДж/Н.

Энергия частицы реальной жидкости (газа), движущейся в по­токе, не будет оставаться постоянной- Часть энергии будет расхо­доваться (переходить в тепловую энергию) на преодоление сопро­тивлений, возникающих вследствие вязкости.

Уравнение Бернулли при условии учета потери напора h_п мо­жет быть представлено в следующем виде:

где p_z — давление атмосферы на том же уровне z, где протекает исследуемый поток с характеристиками w, у и р.

После преобразования уравнение Бернулли выражается в виде постоянства суммы напоров: геометрического h_геом, статического (пьезометрического), динамического h_дин и потерь h_п

При движении газов в трубопроводах происходят постоянные превращения напоров. Если говорить об изотермическом течении газа, то превращения напоров обратимы за исключением того, что теряется, причем на потери расходуется напор динамический, который при движении газа постоянно возобновляется за счет имеющегося запаса статического напора.

Важнейшей инженерной задачей является сведение к миниму­му потерь напора при движении газа. Поэтому изучение причин потерь напора является весьма важным.

Схема изменения напоров при протекании потока газа по трубо­проводу переменного сечения (к выводу уравнения Бернулли)

Теорема импульсов Эйлера (приводится без вывода) имеет важное значение для некоторых инженерных расчетов, так как она позволяет анализировать явления, происходящие в некото­рой, выделенной из общего потока области, по данным, относя­щимся к воображаемой поверхности, ограничивающей эту область. Формулировка теоремы импульсов такова: изменение импульса всех сил какой-нибудь области газа, ограниченной воображаемой кон­трольной поверхностью, отнесенного к единице времени, равно результирующей внешних сил, действующих на данную поверх­ность. Если движение газа установившееся, то изменение импуль­са сил массы газа обусловлено только перемещением в единицу времени объема газа, ограниченного контрольной поверхностью. Также изменение полного импульса сил, вызванное перемещени­ем газового объема, равно результирующей импульсов сил, про­ходящих в единицу времени через неподвижную в пространстве контрольную ограничивающую поверхность. Математически тео­рема импульсов может быть записана в следующем виде:

где т — масса газа; Р— внешняя сила, действующая на поверхность. Теорема импульсов вытекает и из теоремы механики твердого тела о количестве движения системы материальных точек. Практи­ческое применение теоремы импульсов дается далее.

Дата добавления: 2014-01-14