Теория подобия

Физическое моделирование.

Математическое моделирование.

Математическое моделирование – исследование процессов или явлений на основе математических моделей.

Математической моделью процессов является исчерпывающее математическое описание процессов переноса. Но эти модели сложные, уравнения, в основном, не решаются. Поэтому их упрощают, путём оценки значимости их членов. Если этот способ невозможен (члены уравнения одного порядка), то сознательно огрубляют исчерпывающее описание процесса. Например, трёхмерное описание приводит к одномерному – от входа в аппарат к выходу. При этом коэффициенты переноса заменяются на неких параметры модели. Отыскание этих параметров, т.е. идентификация модели, проводят путём составления физического и численного экспериментов.

Любая модель неполно отражает оригинал. Поэтому следующим этапом моделирования является проверка адекватности модели – соответствия её моделируемому объекту. Это достигается путём сопоставления результатов моделирования с численным либо физическим экспериментом.

Если модель в недостаточной степени соответствует оригиналу, проводят её коррекцию.

Конечным этапом математического моделирования является использование полученной модели для описания объекта, либо уже существующего, либо проектируемого.

Итак, этапы математического моделирования:

– составление математической модели;

– идентификация модели;

– проверка адекватности модели, при необходимости коррекция;

– использование модели для описания объекта-оригинала.

Современное материальное обеспечение математического моделирования – компьютеры, возможности которых велики.

Физическое моделирование проводится на основе экспериментального изучения материальных моделей объекта. При этом возникают три проблемы:

- какую модель использовать (форма, размер, среда);

- какие характеристики измерять;

- как перенести результаты исследования с модели на объект.

Эти проблемы решаются с помощью теории подобия, являющейся теоретической основой физического моделирования.

Подобие в широком смысле – это возможность распространения результатов экспериментов с модели на оригинал. В узком смысле подобие – это тождественность описания полей соответствующих величин модели и оригинала в обобщённых переменных или, по-другому, постоянство отношения сходственных величин модели и оригинала. Далее «подобие» будем понимать в узком смысле.

Подобные объекты описываются одной системой дифференциальных уравнений и имеют подобные условия однозначности (геометрическое подобие, временное подобие, подобие физических величин, подобие начальных и граничных условий).

Геометрическое подобие – постоянство отношения всех сходственных линейных размеров модели и оригинала.

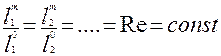, (2.88)

где l и l – сходственные линейные размеры модели и объекта, K – константа геометрического подобия.

Временное подобие (гомохронность) – постоянство отношения сходственных интервалов времени модели и оригинала:

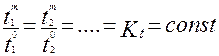, (2.89)

Если 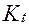=1, то имеем синхронность.

Подобие физических величин - постоянство отношения физических величин для модели и оригинала в сходственных точках сходственного момента времени:

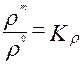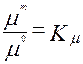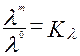, , (2.90)

Подобие модели и объекта предполагает подобие полей физических величин:

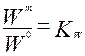- гидродинамическое подобие (подобие полей скоростей)

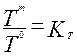- тепловое подобие (подобие полей температуры)

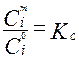- концентрац. подобие (подобие полей концентраций)

При соблюдении геометрического и временного подобия будет соблюдаться также подобие полей скоростей, температур, концентраций и других физических величин.

Подобие начальных условий – подобие полей всех физических величин в начальный момент времени.

Подобие граничных условий – постоянство отношения соответствующих величин на границах модели и оригинала.

Константы подобия – отношения одноимённых величин модели и оригинала. Они постоянны для различных сходственных точек подобных систем.

Инварианты подобия – безразмерные отношения величин, характеризующих модель или оригинал.

Симплексы подобия – инварианты подобия, представляющие собой отношения однородных величин:

(2.91)

Критерии подобия – инварианты подобия, представляющие собой отношения разнородных, сложных величин. Например:

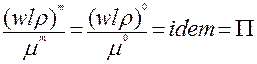(2.92)

Определяющие критерии подобия составлены из величин, входящих в условия однозначности. Определяемые критерии подобия содержат величины, которые необходимо определить.

Наиболее простой метод получения критериев подобия заключается в следующем: дифференциальное уравнение приводится к безразмерному виду делением всех членов на один из них. Полученные комплексы являются критериями подобия.

Теоремы подобия:

1. Подобные объекты характеризуются численно равными критериями подобия.

2. Решение дифференциального уравнения (уравнений) описывающего объект, может быть представлено в виде зависимости между критериями подобия.

3. Объекты подобные, если они описываются одной системой дифференциальных уравнений, имеют подобные условия однозначности и их определяющие критерии равны.

Математическая зависимость между критериями и симплексами подобия, характеризующими данный процесс переноса субстанции, называется критериальным уравнением:

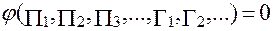(2.93)

Если определяемый критерий, то имеем:

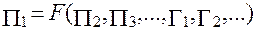(2.94)

Обычно критериальные уравнения имеют вид степенной зависимости:

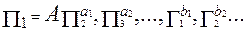(2.95)

Величины 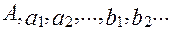- определяются экспериментально. Если какой – либо из определяющих критериев слабо влияет на определяемый критерий, то его исключают из уравнения.

Дата добавления: 2014-01-14