Подобие гидромеханических процессов

Запишем для вертикальной оси z уравнение Навье – Стокса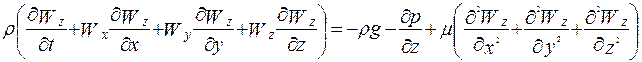

(2.96)

Уравнение (2.96) преобразуем следующим образом: отбросив знаки математических операторов, делим одну часть уравнения на другую и находим критерии подобия:

(I)

(II)

(III)

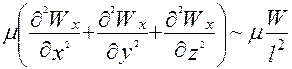(IV)

(V)

Члены в правой части уравнения разделим на :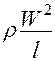

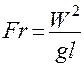; – Критерий Фруда (2.97)

Этот критерий отображает влияние сил тяжести на движение жидкости, является отношением сил инерции и тяжести.

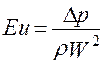; – Критерий Эйлера (2.98)

Критерий Эйлера – является мерой отношения сил поверхностного давления и инерции.

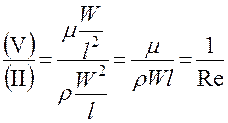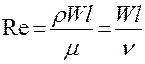; – Критерий Рейнольдса (2.99)

Критерий Рейнольдса – Является мерой отношения сил инерции и вязкого трения.

Внутри левой части уравнения имеем:

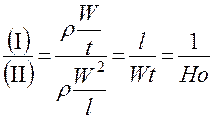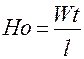; – Критерий гомохронности для

неустановившегося движения (2.100)

Все критерии, симплексы, константы, подобия безразмерные величины.

Для гидродинамического подобия:

Γi = idem(i = 1, 2…n), Re = idem, Eu = idem, Fr = idem, Ho = idem. (2.101)

Решение уравнения Навье – Стокса может быть представлено критериальным давлением вида:

f (Re, Ho, Eu, Fr) = 0 (2.102)

В ряде случаев (течение жидкости по трубе, например) последнее уравнение должно быть дополнено симплексами подобия:

f (Re, Ho, Fr, Eu, Гi) = 0 (2.103)

Обычно определяют ∆p, тогда:

Eu = f (Re, Ho, Fr, Гi) (2.104)

Для установившихся процессов критерий гомохронности Ho = 0 и должен быть исключён из уравнений, а критерием Fr можно пренебречь вследствие того, что сила тяжести мала по сравнению с силами инерции и вязкого трения. Таким образом, зависимость (2,104) сводится к виду:

Eu = f (Re, Гi) (2.105)

При развитых турбулентных режимах, в зоне автомодельности сопротивления трения по критерию Re, зависимость ещё более упрощается и принимает вид:

Eu = f (Гi) (2.106)

Результаты экспериментальных данных обрабатываются, обычно, в виде степенной зависимости:

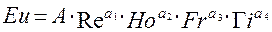(2.107)

Рассмотрим подобие граничных условий. Вязкий поток импульса через границу раздела фаз 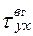можно определить по закону Ньютона:

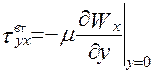(2.108)

Тот – же поток можно выразить в виде линейной зависимости от разности на границе и в ядре потока среды:

(2.109)

Здесь 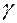– коэффициент импульсоотдачи.

Тогда получим:

(2.110)

Проведя формальное преобразование получим:

(2.111)

Здесь – характерная линейная величина, 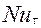– гидродинамический критерий Нуссельта. Гидродинамический критерий Нуссельта является безразмерной формой коэффициента импульсоотдачи. Поскольку поле скорости 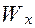однозначно определяет коэффициент γ, решение уравнений Навье – Стокса можно представить следующим образом:

(2.112)

Для многих практически важных случаев число определяющих критериев может быть сокращено. Влиянием силы тяжести на 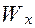зачастую можно пренебречь и подключить критерия Фруда. Для стационарных процессов исключается критерий гомохронности. Процесс импульсоотдачи может стать автомодельным и по отношению к критерию Рейнольдса.

Дата добавления: 2014-01-14